
Part 5 of 5
Part 1: Astronomical cycles
Part 2: Science, psychics and myths
Part 3: Poleshifts and theosophy
Part 4: Climate change
Part 5: Appendices
1. The zodiac and precession
2. The zodiac and cataclysms
3. Herodotus and the Egyptians
4. Three axial inversions?
5. The Dendera zodiacs
6. Sampson Arnold Mackey
In a footnote to the first part of her article ‘The esoteric character of
the Gospels’, published in November 1887, H.P. Blavatsky wrote:
There are several remarkable cycles that come to a close at the end of this century. First, the 5,000 years of the Kaliyuga cycle; again the Messianic cycle of the Samaritan (also Kabalistic) Jews of the man connected with Pisces (Ichthys or ‘Fish-man’ Dag). It is a cycle, historic and not very long, but very occult, lasting about 2,155 solar years, but having a true significance only when computed by lunar months. It occurred 2410 and 255 BCE, or when the equinox entered into the sign of the Ram, and again into that of Pisces. When it enters, in a few years, the sign of Aquarius, psychologists will have some extra work to do, and the psychic idiosyncrasies of humanity will enter on a great change.1
According to the canonical, occult figures for the precession of the equinoxes, the vernal equinox falls back 50 seconds of arc a year, and therefore takes 2160 years to move through one constellation of the zodiac (30°), and 25,920 years for a complete circuit of the zodiac. In reality, the rate of precession varies. Blavatsky used the figure of 50.10 seconds of arc per year, equivalent to 25,868 years for a complete precessional cycle.2 Dividing the latter figure by 12, gives (in round figures) 2155 years as the length of a messianic cycle. The rate of precession for the epoch J2000.0 is 50.288 arc-seconds per year, and the rate is said to be increasing by 0.00024 arc-seconds per year.
It should be noted that the constellations of the zodiac do not really extend over exactly 30° of the ecliptic; they are of varying sizes, and some of them overlap in the sense that some lines of ecliptic longitude pass through two zodiacal constellations. In addition, there is a gap between Scorpio and Sagittarius, where the ecliptic passes through the southern part of a thirteenth constellation, Ophiucus, the Serpent Bearer.
The kali-yuga began in February 3102 BCE, and the first 5000 years therefore came to an end in February 1899 (= 5000 - 3102 + 1).3 Blavatsky suggests that the Piscean Age also came to a close at the end of the 19th century. She indicates that 2155 years elapsed between the start of the Age of Aries in 2410 BCE and the start of the Piscean Age in 255 BCE. If the Piscean Age also lasted 2155 years, the Aquarian Age would have begun in 1901 (= 2155 - 255 + 1) if 255 BCE is a chronological date, or 1900 if it is an astronomical date. On the basis of the current rate of increase in precession, the Piscean Age would have lasted 2157 years (assuming that Pisces covers 30° of arc).
The dates of 2410 BCE and 255 BCE are also given by Gerald Massey and quoted by Blavatsky in her article ‘Esotericism of Christian dogma’, published in December 1887.4 Elsewhere Blavatsky quotes slightly different figures. In The Secret Doctrine she makes two references to C.F. de Volney’s remark that Aries was in its 15th degree in 1447 BCE.5 This is just over 100 years earlier than the date of 1333 BCE that we would expect on the basis of her own/Massey’s figures. She also quotes on several occasions from A.H. Sayce, who says that the Age of Taurus began around 4700 BCE and the Age of Aries in 2540 BCE.6 These dates are about 130 years earlier than those given by Blavatsky.
According to one astronomy book, the Age of Aries began around 2100 BCE, the Age of Pisces around the start of the Christian era, and the Age of Aquarius will begin around the year 2200.7 These dates are about 300 years later than those given by Blavatsky. The astronomical date given for the beginning of the Age of Aquarius by the French Institut Géographique National is 2010. Schwaller de Lubicz gives a date of 2100. Clearly there is no consensus on where to place the boundary between Pisces and Aquarius and thus on how best to divide the zodiac into 12 equal segments of 30°.
Taking the position of the equinox in 2410 BCE as the boundary between Taurus and Aries (as Blavatsky does) is certainly a reasonable way of fitting an artificial zodiac of 12 equal constellations to the actual zodiac, though it places the Pleiades star cluster (which forms part of the Taurus constellation) in Aries, but within 1.5° of the border with Taurus. F.J. Dick proposed that Alcyone (the chief star of the Pleiades) should be seen as marking the boundary between Taurus and Aries,8 in which case the Age of Aries would have begun around 2335 BCE (based on the rigorous formula for precession and correcting for proper motion). Taking Alcyone as 0° Taurus would place Regulus at 0° Leo, Antares at 9° Scorpio, and Fomalhaut at 4° Aquarius, these being the four royal stars of the Persians. In this zodiac, the Age of Aquarius would have begun around 1975.
Blavatsky says that at the beginning of the kali-yuga, in 3102 BCE, the vernal equinox fell within the constellation Taurus.9 A more precise reference is provided in The Secret Doctrine, where J.S. Bailly is quoted as saying that at the beginning of the kali-yuga the vernal equinox approximately coincided with the Eye of the Bull (Aldebaran).10 Blavatsky supports this view when she says that Aldebaran was also in conjunction with the vernal equinoctial point about 31,000 years ago, and she adds: ‘It is from this point of the ecliptic that the calculations of the new cycle were commenced.’11 The figure of 31,000 years is approximately equivalent to 3102 BCE plus a complete precessional cycle (3102 + 1888 + 25,920 - 1 = 30,909). Using the rigorous precession formula, Aldebaran was aligned with the equinox in 3045 BCE, and assuming a rate of precession of 50" per year and a shift in the axis of 4° every 25,920 years, it would also have coincided with the equinox in 30,920 BP (counting from J.2000.0).
Based on the actual position of the vernal equinoctial point among the zodiac constellations, J.B. Kaler stated that the Age of Taurus began around 4500 BCE, the Age of Aries in 2000 BCE, and the Age of Pisces in 100 BCE, and that the Age of Aquarius will begin around 2700 CE.12
In 255 BCE, the date given by Blavatsky for the start of the Piscean Age, the vernal equinoctial point lay 2.6° west of Beta Arietis.13 Pisces extends over a total of about 40°, and only if we regard it as covering 30° would the Aquarian Age have begun around 1900. The position of the vernal equinox in 2022 is shown in fig. 1; clearly, it is still well within Pisces. It will be several hundred years before the vernal equinox conjuncts the main stars of Aquarius (i.e. before their ecliptic longitude is 0º). If we consider stars up to the 6th magnitude, the equinox will conjunct the first star of Aquarius in 2363. If we only consider stars up to the 5th magnitude, the equinox will coincide with the first star, Omega2 Aquarii, in about 2700, as shown in fig. 2. The vernal equinox will not conjunct the last bright star in Pisces (Beta Piscium) until 2815.

Fig. 1. Position of the vernal equinox in 2022,
showing the celestial equator (red), ecliptic coordinate
grid
(green), Pisces and Aquarius, and their boundaries as recognized by modern astronomy.
(CyberSky 5.2)

Fig. 2. Position of the vernal equinox in 2700. Omega2 Aquarii is marked with a cross. (CyberSky 5.2)
We are currently in a period of transition to the Aquarian Age. It should
be borne in mind, however, that the sun, as viewed from earth, passes through all the
constellations of the zodiac every year. And that the zodiacal age takes
its name from the constellation the sun is in
at the time of the spring equinox
in the northern hemisphere. If we chose the autumn equinox or the
summer or winter solstice instead, the present age would have a different
name, just as it would if we adopted a southern-hemisphere
perspective. Clearly, the present Piscean Age does not mean that only Piscean
influences are at work.
Notes
1. H.P. Blavatsky Collected Writings, Theosophical Publishing House (TPH), 1950-91, 8:174fn.
2. H.P. Blavatsky, The Secret Doctrine, Theosophical University Press (TUP), 1977 (1888), 2:330fn. Her source is: Alexander Winchell, World-Life, or Comparative Geology, 1883, p. 285 (see Secret Doctrine References).
3. It is necessary to add ‘1’, because in the historical or chronological method of counting, as opposed to the astronomical method of counting, there is no year zero between 1 BCE and 1 CE. Some authors say that the kali-yuga began in 3101 BCE, this being the equivalent date using the astronomical system. Either way, the year 1 CE was not the 3103rd year of the kali-yuga but the 3102nd (see Subba Row, Esoteric Writings, Theosophical Publishing House, 1931, p. 55). J.S. Bailly clearly indicates that 3102 BCE is a chronological date when he says that 4383 years (and not 4384) elapsed between 3102 BCE and 1282 CE (The Secret Doctrine, 1:666-7).
4. Blavatsky Collected Writings, 8:384. Massey says that the 255 BCE date is given by the French astronomer Cassini and by Sir William Drummond (Gerald Massey, ‘The prehistorical period of man in Egypt and Africa’, in: Brad Steiger & John White, Other Worlds, Other Universes, Health Research, 1986, pp. 48-62).
5. The Secret Doctrine, 1:658, 2:436fn.
6. The Secret Doctrine, 2:693; A.H. Sayce, Astronomy & Astrology of the Babylonians (1874), Wizards Bookshelf, 1981, p. 237.
7. Elisabeth Mulder, Zon, maan en sterren, Christofoor, 1991, p. 47.
8. ‘Ancient astronomy in Egypt and its significance’, The Theosophical Path, March 1916, pp. 287-303 (p. 299).
9. H.P. Blavatsky, Theosophical Glossary, Theosophy Company, 1973 (1892), p. 387.
10. The Secret Doctrine, 1:663.
11. The Secret Doctrine, 2:785. A figure of 31,105 years is also given (1:435).
12. James B. Kaler, The Ever-changing Sky: A guide to the celestial sphere, Cambridge University Press, 2002 (1996), p. 152.
13. G. de Purucker stated that around 1935 the vernal equinox was in approximately the 11th degree of the constellation Pisces (Fountain-Source of Occultism, TUP, 1974, p. 673). This can be explained as follows: The vernal equinox is said to have coincided with the initial point of the Hindu zodiac in 560 CE (E. Burgess & W.D. Whitney, Surya-Siddhanta (1860), Wizards Bookshelf, n.d., pp. 323, 326); according to the rigorous formula for precession and also CyberSky 5.2, the actual date was 564 CE. Using the same formula, from 564 CE to 1935 the equinox shifted 19.089°, so if we take the position of the equinox in 564 AD as 0° Aries/30° Pisces, the equinox would have been at 30-19.089 = 10.9° Pisces (i.e. in the 11th degree) in 1935.
Cataclysms are said to occur at every renewal of the precessional
cycle.1 The point
in the zodiac from which a
precessional cycle is measured can apparently vary; at present it appears to
be measured from 6.4° Cancer (see part 3, section 4). Some of the catastrophes
on which data are available are mentioned below. It appears that earth changes
can take place at any point in the precessional cycle, and the data are not sufficient
to identify any overall patterns. For instance, different constellations may
favour different types of catastrophe. Also, the circle of the zodiac could be
divided into four quarters (corresponding to the four seasons), with the boundaries
being marked by Aries (vernal equinox), Capricorn (summer solstice), Libra (autumnal
equinox) and Cancer (winter solstice), and it is possible that cataclysms accompanying
the equinox’s entry into each quarter are severer than normal. Bear in
mind, though, that the probability of a cataclysm occurring in one of these
four constellations by chance is as high as 1 in 3.
A large island, Ruta, in the Pacific Ocean is said to have sunk 859,000 years ago.2 At that time the vernal equinoctial point would have been at 19° Aries. The smaller island of Daitya in the Indian Ocean is said to have sunk 270,000 years ago,3 when the equinox would have been at 28.5° Cancer.
The approximate dates on which the last nine zodiacal ages began are as follows: Libra 17,380 BP (before present, i.e. 2000), Virgo 15,220 BP, Leo 13,060 BP, Cancer 10,900 BP, Gemini 8740 BP, Taurus 6580 BP, Aries 4420 BP (2420 BCE), Pisces 255 BCE, Aquarius 1900.
The melting of the ice sheets at the end of the last ice age led to a significant rise in world sea levels. This was not a gradual process; three sudden ice-melts and the collapse of glacial lakes resulted in three episodes of rapid flooding, as tens of thousands of cubic kilometres of water rushed off the polar ice caps generating earthquakes and superwaves. The three floods began about 14,000, 11,500 and 8000 years ago, and the resulting 120-metre rise in sea level destroyed many coastal settlements.4
Blavatsky refers to a deluge in Central Asia 10-12,000 BP, which changed the whole face of Central Asia, and transformed the present Gobi Desert into a sea for the last time.5 Poseidonis, an island about the size of Ireland situated in the mid-Atlantic (one of the last major remnants of Atlantis), sank ‘in a single day and night’ in 9565 BCE,6 when the equinox was at about 9° Leo. Cro-Magnon man started to appear on the western coasts of Europe and around the shores of the Mediterranean about 40,000 years ago, and arrived in large numbers between 15,000 and 10,000 BP. One theory is that they were migrants from Poseidonis and other islands in the Atlantic, who emigrated in several waves as their homelands showed increasing signs of sinking.7
One Sumerian text seems to say that the Deluge occurred in the Age of Leo.8 The Egyptian Pyramid Texts, too, associated a period of terrible destruction, including a flood, with the Age of Leo.9 Immense floods swept repeatedly down the Nile valley between 15,000 and 11,500 BP, reaching a climax around 12,500 BP.10
Turning to more recent times, there was a major flood in Sumer around 5000-4800 BP, probably resulting from the Tigris and Euphrates rivers drastically changing their courses and overflowing their banks.11 This was towards the end of the Age of Taurus. However, according to another interpretation, the very thick silt deposit at Ur may have been laid down during a marine incursion 7500-5500 BP due to the rising sea level.12
Noah’s flood is dated by Ussher’s biblical chronology at 2349 BCE, but there was certainly no worldwide flood at that time. Blavatsky says that Noah’s flood is ‘a purely mythical rendering of old traditions’, and that ‘as described in its dead letter and within the period of Biblical chronology’, it ‘never existed’ but is ‘a fiction based upon geological and geographical ignorance’.13 She says that the Biblical deluge relates to the partial flood which changed the whole face of Central Asia about 10,000 BCE.14 The Age of Aries did, however, witness numerous natural disasters.
According to Chinese chronology, disastrous floods occurred in China in 2953 BCE, 2357-2205 BCE, and 1766 BCE.15 There was a great inundation in China in 2297 BCE, in the 61st year of the reign of Yao.16 There were major floods in Babylon in 2379 BCE and Palestine in 2355 BCE.17 Volcanic eruptions followed by radical climatic changes are thought to have precipitated the collapse of the Mesopotamian empire of Akkad, sometime after 2290 BCE.18
The vast Thar or Great Indian Desert to the east of the Indus river was once traversed by a great river, known in Vedic writings as the Sarasvati (an extension of the present-day Ghaggar or Hakra river). This once fertile region was a key centre of early Indic civilization. Around 1900 BCE, in the Age of Aries, a series of tectonic upheavals caused several rivers to change their courses, leading to devastating floods and the drying up of the Sarasvati and other rivers. As a result, Indic civilization was temporarily eclipsed, and its centre shifted eastward to the Ganges and Yamuna valleys.19
The Minoan civilization in the Aegean was devastated by fire, flooding and ash, following a series of volcanic eruptions on the island of Thera (Santorini), 125 km to the north of Crete, the final explosion being dated at 1628 BCE.20 Manetho’s king list dates the flood of Deucalion to the reign of the sixth king of the 18th dynasty, or about 1500 BCE.21 (Plato, however, says that it followed the sinking of Poseidonis.) Around 1250 BCE, extensive flooding seems to have occurred in Anatolia (modern Turkey), burying the Bronze Age city of Tiryns, and at about the same time the rich merchant city of Troy (archaeological level VI) was destroyed by an earthquake.22
The tree-ring record for the past 5000 years points to global environmental traumas between 2354 and 2345 BCE, 1628 and 1623 BCE, 1159 and 1141 BCE, 208 and 204 BCE, and 536 and 545 CE. The first three fall within Blavatsky’s dates for the Age of Aries. These five episodes coincide with the onset of ‘dark ages’ for society. They involved earthquakes, tidal waves, volcanic eruptions, and ocean floor outgassing.23
Natural disasters have of course continued into more recent times. The most devastating earthquakes in terms of human fatalities include: 526 CE, Antioch, Syria, 250,000 deaths; 1201, Upper Egypt or Syria, 1,100,000 deaths; 1556, Shensi province, China, 830,000 deaths; 1737, Calcutta, India, 300,000 deaths. The eruption of Vesuvius, Italy, in 79 CE buried the cities of Pompeii and Stabiae under ashes and Iapilli and Herculaneum under a mudflow, and killed about 16,000 people. An eruption of Kelud, Java, Indonesia, in 1586 killed 10,000 people. The eruption of Etna, Italy, in 1669 left 20,000 people dead. A tidal wave (tsunami) following an eruption of Tambora, Sumbawa, Indonesia, in 1815 killed 56,000 people. In 1703 a tsunami hit Awa, Japan, killing more than 100,000 people. The 1883 eruption of Krakatoa, Krakatau, Indonesia, was one of the most catastrophic in history. A series of tremendous explosions occurred, the largest being heard at a distance of 4670 km. Most of the 36,000 people killed on Java and Sumatra were drowned by tidal waves as high as 35 metres.24
In the 20th century, the worst flooding disasters (in terms of human fatalities) occurred in China: 1931, 3.7 million dead; 1938, 500,000 dead; 1939, 500,000 dead; 1959, 2.9 million dead. The worst earthquakes also occurred in China: 1920, 180,000 dead; 1927, 200,000 dead; 1976, 242,000 dead. The worst hurricanes or typhoons were: China, 1922, 100,000 dead; Bangladesh, 1991, 138,866 dead; and Bangladesh, 1970, 300,000 dead.25 The three worst natural disasters so far in the 21st century were: Cyclone Nargis, Myanmar, May 2008, 146,000 dead; the Indian Ocean Tsunami, December 2004, 230,000 dead; and the Haiti earthquake, January 2010, 316,000 dead.26
G. de Purucker says that the great tidal waves and earthquakes occurring in the last few thousand years are premonitions of what in a few more thousand years will occur with augmented force.27 Major cataclysms are forecast in about 16,000 years,28 when the equinox will lie in the middle of Cancer.29 The European cataclysm will see the submersion of the British Isles, most of France, the Netherlands, some of Spain, and a good deal of Italy. It will not take place in a night, but will be preceded by slow subsidence of the coast and major earthquakes.
Notes
1. H.P. Blavatsky, The Secret Doctrine, TUP, 1977 (1888), 1:649. ‘... the weal and woe of nations is intimately connected with the beginning and close of [the precessional] cycle’ (2:330). Blavatsky also refers to a cycle of 21,000 years (see part 1, section 5 of this article), saying that a minor cataclysm occurs after the first half-cycle of 10,500 years, and a universal cataclysms after the second (H.P. Blavatsky, Isis Unveiled, TUP, 1972 (1877), 1:30-1; H.P. Blavatsky Collected Writings, TPH, 1950-91, 3:150).
2. Letter from H.P. Blavatsky to J.R. Skinner, 17 February 1887. The figure usually given is 850,000 years, when the equinoctial point would have been in the middle of Sagittarius. However, Ruta’s submergence is said to have taken 150,000 years (The Secret Doctrine, 2:395, 751) – enough time for nearly six complete circuits of the zodiac!
3. The Secret Doctrine, 1:650-1; G. de Purucker, Studies in Occult Philosophy, TUP, 1945, pp. 19, 24.
4. Stephen Oppenheimer, Eden in the East, Weidenfeld & Nicolson, 1998, pp. 18, 29-38.
5. The Secret Doctrine, 2:5, 141; Isis Unveiled, 2:426.
6. The Mahatma Letters to A.P. Sinnett, TUP, 2nd rev. ed., 2021, pp. 151/155.
7. See The ancient Americas, section 8, davidpratt.info.
8. Zecharia Sitchin, The 12th Planet, Avon Books, 1976, p. 409.
9. Graham Hancock, Fingerprints of the Gods, Heinemann, 1995, pp. 370-2.
10. Fingerprints of the Gods, pp. 411-2, 414.
11. Paul Dunbavin, The Atlantis Researches, Third Millennium, 1995, p. 101.
12. Eden in East, pp. 49-62.
13. The Secret Doctrine, 1:370, 2:141, 393; Blavatsky Collected Writings, 5:199fn.
14. Isis Unveiled, 2:426.
15. The Atlantis Researches, pp. 114-5.
16. Charles Gould, Mythical Monsters (1886), Wizards Bookshelf, 1981, pp. 129-30.
17. James DeMeo, Saharasia, Orgone Biophysical Lab. Inc., 1998, p. 321.
18. Georg Feuerstein, Subhash Kak & David Frawley, In Search of the Cradle of Civilization, Quest, 1995, p. 84.
19. In Search of the Cradle of Civilization, pp. 87-99.
20. In Search of the Cradle of Civilization, pp. 83-4.
21. The Atlantis Researches, p. 102.
22. In Search of the Cradle of Civilization, p. 83.
23. New Scientist, 9 Jan. 1999, p. 42.
24. Encyclopaedia Britannica, CD98.
25. disastercenter.com/disaster/TOP100K.html.
26. tiptoptens.com/2011/03/28/10-worst-natural-disasters-of-21st-century.
27. G. de Purucker, Fundamentals of the Esoteric Philosophy, TUP, 2nd ed., 1979, p. 316.
28. The Secret Doctrine, 2:330-1; Studies
in Occult Philosophy, pp. 35-9, 41, 485-6, 702-3; G. de Purucker, Fountain-Source
of Occultism, TUP, 1974, pp. 163-4; Fundamentals of
the Esoteric Philosophy, pp. 280/2; G. de Purucker, Occult Glossary,
TUP, 2nd ed., 1996, p. 143.
Blavatsky refers to the ‘great year’ of
the Chaldeans, lasting about 21,000 years. She says that major cataclysms occur
at the end of each cycle, and minor cataclysms at the midpoint. In this connection
she mentions R. Falb’s theory that there was a ‘universal’ deluge
in 4000 BCE, and that the next such disaster will occur in 6500 CE. The catastrophe
after that would therefore occur in 17,000 CE (Blavatsky Collected Writings,
3:149-50; Isis Unveiled, 1:30-1).
29. The symbol for Cancer looks like ‘69’ (♋). In this connection, the following may be significant: Blavatsky says that the figures of a man standing upright and a woman standing on her head before him symbolize the poles inverted. The Persian sovereign, King Cambyses, is said to have burst out laughing when he entered the Temple of the Kabiri in Egypt and saw the figures of a man and woman (the two Kabiri) represented in this position. The Kabiri are, among other things, the ‘Deluge’ gods (The Secret Doctrine, 2:360). Could this mean that when the earth is in Cancer it is more susceptible not to complete axial inversions, but to major disturbances of the axis? It should be noted, however, that the Kabiri are also associated with the two Dioscuri, Castor and Pollux (The Secret Doctrine, 2:362), which are situated in the adjacent constellation of Gemini.
In The Secret Doctrine we find four different versions of certain remarks – possibly
relating to poleshifts – that the Egyptian priests made to Herodotus in the 5th century BCE.
Only one of these versions is strictly accurate.
On one occasion Blavatsky states that the Egyptian priests told Herodotus that the sun had not always risen where it now rises and that in former times the ecliptic had cut the equator at right angles.1 At that time the earth would have been lying on its side with its poles in the plane of the ecliptic. She refers in a footnote to Bailly’s Histoire de l’Astronomie Ancienne, where the statement is attributed to Herodotus’ History, Book II (Euterpe), 142. But if we look up this reference, we find that what Herodotus actually said was the following: ‘The sun, however, had within this period of time [341 generations], on four several occasions, moved from his wonted course, twice rising where he now sets, and twice setting where now he rises.’2 There is no reference here to either the equator or the ecliptic, though obviously to become inverted the poles would have to pass through the plane of the ecliptic, at which time the ecliptic would cut the equator at right angles. Herodotus converts the figure of 341 generations into a period of 11,340 years.
On another occasion Blavatsky says that the Egyptian priests told Herodotus that the pole of the earth and the pole of the ecliptic had formerly coincided,3 i.e. that the poles had been perpendicular to the ecliptic. She does not give a source for this remark, but it is probably S.A. Mackey.4
Elsewhere Blavatsky states that the Egyptian priests told Herodotus that ‘even since their first Zodiacal records were commenced, the Poles have been three times within the plane of the Ecliptic, as the Initiates taught.’5 She also says that ‘even since the time of the regular establishment of the Zodiacal calculations in Egypt, the poles have been thrice inverted.’6 If three 360° inversions of the axis are being referred to, ‘within the plane of the ecliptic’ would have to mean ‘below the plane of the ecliptic’ (i.e. a tilt of between 90° and 270°) for the two statements to be consistent; if it means that the poles lay in the plane of the ecliptic (i.e. that the tilt was either 90° or 270°), they would not be consistent as the north pole would pass twice through the ecliptic in each 360° inversion of the axis. If three 180° inversions are being referred to, ‘three times within the plane of the ecliptic’ can be interpreted quite literally to mean that the poles have passed through the ecliptic three times.
Another (accurate!) reference to Herodotus is quoted by Blavatsky from Gerald Massey, who wrote: ‘The priests informed the Greek inquirer that time had been reckoned by them for so long that the sun had twice risen where it then set, and twice set where it then arose.’ According to Massey, ‘This ... can only be realized as a fact in nature by means of two cycles of Precession, or a period of 51,736 years [= 2 x 25,868].’7 For Massey, then, this change is not the result of an inversion of the poles, but is purely an effect of the precession of the equinoxes.
On any particular day, the sun rises and sets against the backdrop of the same constellation. At dawn an observer looks towards the east to see the sun come up. By dusk, the earth has rotated 180�, and the observer looks towards the west to see the sun go down – in the direction of exactly the same constellation as at dawn. From month to month, as the earth orbits the sun, the sun appears to move through the 12 constellations of the zodiac. However, the earth does not revolve through a full 360°� from one spring (or autumn) equinox to the next, or from one summer (or winter) solstice to the next, but through about 50 arcseconds less, due to precession. If, at the spring equinox, the sun rises and sets in Pisces, then half a precessional cycle later, it will rise and set in Virgo, since these two constellations lie opposite one another. The expression concerning the sun rising where it once set is therefore somewhat misleading.

Fig. 1.
R.A. Schwaller de Lubicz gives a similar interpretation to Massey, but correctly says that only one and a half precessional cycles would be required to produce the effect referred to: Herodotus’s remarks mean that ‘the vernal point had twice been located in the same constellation of Aries, and that it also passed twice in the opposing constellation of Libra. This would grant the duration of one and a half precessional cycles to the entire historic and prehistoric periods, or approximately 39,000 years.’8
In Herodotus’s time the vernal sunrise (and sunset) occurred in Aries, with Libra in opposition (due west). 13,000 years before that (half a precessional cycle), the vernal sunrise (and sunset) occurred in Libra, with Aries in opposition. Counting back another 13,000 years, the vernal sunrise would have occurred in Aries, and 13,000 years before that in Libra. Thus, in the preceding 39,000 years the vernal sunrise/sunset has occurred twice in Libra and twice in Aries.
The figure of 39,000 years accords closely with the testimony of the Turin Papyrus, which shows that the ancient Egyptians considered their prehistory to go back 36,620 years before Menes (c. 4240 BCE), or about 40,000 years before our era. Diodorus Siculus reports that according to several chroniclers, gods and heroes ruled Egypt for 18,000 years, following which the land was governed by mortal kings for 15,000 years, bringing the time span of history and prehistory to a total of 33,000 years. Manetho grants 15,150 years to the divine dynasties and 9777 years to all kings who had reigned before Menes, giving a total of 24,927 years to prehistory. George the Syncellus states that the Egyptians had an ancient chronicle that mentioned 30 royal dynasties preceded by the reign of the gods, comprising a period of 36,525 years (25 sothic cycles of 1461 years).9
W. Marsham Adams, following Rawlinson, gives yet another interpretation of the remarks reported by Herodotus. In his view, they refer to the sothic cycle and the heliacal risings and settings of the star Sirius (Greek: Sothis; Egyptian: Sepdet). (The heliacal rising of a star means that it rises just before the dawn, so that it is visible very briefly before being lost in the solar rays.) The Egyptians had a civil or vague year of 365 days, and a fixed or sothic year of 365.25 days based on the heliacal rising of Sirius, which approximately coincided with the summer solstice and the rise of the Nile. A sothic cycle commences when the civil and sothic years begin on the same day. The first day of the civil year then falls back in relation to the sothic year by a quarter of a day each year, or one day every four years. The first day of the civil and sothic years will therefore again coincide after 365 x 4 = 1460 sothic years (or 365.25 x 4 = 1461 civil years) – this being the length of the sothic cycle. Adams writes:
Since in the course of the cycle, the heliacal risings take place on each day of the entire year, they will run during the first half of the cycle in one direction (relatively to the earth’s orbit) and in the latter half in the opposite. And since there is also a corresponding series of settings, subject to a similar change of direction, the two series would in each cycle make up a double reversal, interchanging positions not once but twice. ... We learn [from Herodotus], therefore, that two Sothiac cycles (four reversals) had been completed since the institution of the scientific Kalendar; so that the cycle then current in the time of Herodotus would be the third. And as there is evidence that that cycle was completed in A.D. 139, and therefore commenced in 1322 B.C.; at which epoch Sothis rose heliacally at Memphis about a week before the solstice, and the Rising of the river was heralded by the Orient of the star. Hence, therefore, we conclude that the commencement of the first Sothiac cycle and the institution of the scientific Kalendar took place (2 x 1,461 years previously, i.e.) at the summer solstice of 4244 B.C. ...10
All these interpretations are plausible but ignore the figure of 341 generations or 11,340 years given by Herodotus. The possibility that three genuine inversions of the axis are being referred to is considered in Appendix 4.
Notes
1. H.P. Blavatsky, The Secret Doctrine, TUP, 1977 (1888), 2:534.
2. Herodotus, The Histories, translated by G. Rawlinson, Everyman’s Library, 1992, p. 194.
3. The Secret Doctrine, 2:332, 368, 431.
4. Samson Arnold Mackey, Mythological Astronomy of the Ancients Demonstrated (1822/23), Wizards Bookshelf, 1973, p. 2.
5. The Secret Doctrine, 2:353.
6. The Secret Doctrine, 2:368. See Appendix 4, Three axial inversions?
7. The Secret Doctrine, 1:435; G. Massey, The World’s Great Year, Sure Fire Press, 1988, pp. 4-5.
8. R.A. Schwaller de Lubicz, Sacred Science: The king of pharaonic theocracy (1961), Inner Traditions, 1982, p. 87.
9. Sacred Science, pp. 86-7.
10. W. Marsham Adams, The Book of the Master of the Hidden Places, edited by E.J. Langford Garstin, Search Publishing Company, 1933, pp. 109-10.
H.P. Blavatsky writes:
The astronomical records of Universal History ... are said to have had their beginnings with the third sub-race of the fourth root-race or the Atlanteans. When was it? Occult data show that even since the time of the regular establishment of the zodiacal calculations in Egypt, the poles have been thrice inverted.1
There are three possible interpretations of this passage (these interpretations are not mutually exclusive).
(1) Simplicius, in the 6th century CE, wrote that he had heard that the Egyptians had kept records of astronomical observations for a period of 630,000 years.2 However, this only allows enough time for the angle of inclination to change by about 100°. Blavatsky says that the zodiacs in the Egyptian Temple of Dendera show the passage of over three precessional cycles, but during this time the inclination of the axis would have changed by only 12°. Perhaps the word ‘invert’ is not meant literally, and Blavatsky means that the axis has shifted (by four degrees) in each of the last three precessional cycles.
(2) The ancient Egyptians are said to have obtained their zodiac from the Atlanteans of Ruta.3 As for the Atlanteans, we are told that ‘their zodiacal records cannot err, as they were compiled under the guidance of those who first taught astronomy, among other things, to mankind’.4 Perhaps, then, the reference to Egypt is a blind and the three inversions actually refer to the period that has elapsed since the Atlantean zodiac was established in their third subrace. If our fifth root-race originated at the start of the fifth subrace of the fourth root-race,5 the period since the beginning of the third subrace of the Atlanteans would have covered nearly 5 1/2 subraces; each subrace lasts 49 precessional cycles,6 so that the total period would have spanned approximately 260 precessional cycles. Since the earth’s axis takes 90 precessional cycles to invert 360°, it would take 270 precessional cycles for it to undergo three complete inversions.
In the Dendera zodiacs, the constellation Virgo is said to appear three times.7 One interpretation is that this means that the equinox has precessed through these constellations (and in fact all the others too) three times, and that the zodiacs indicate (among other things) the passage of three precessional cycles. This interpretation corresponds to the first interpretation given above. But Blavatsky gives another interpretation:
the three ‘Virgins,’ or Virgo in three different positions, meant, with both [the Hindus and the Egyptians] the record of the first three ‘divine or astronomical Dynasties,’ who taught the third root-race; and after having abandoned the Atlanteans to their doom, returned (or redescended, rather) during the third sub-race of the fifth, in order to reveal to saved humanity the mysteries of their birth-place – the sidereal Heavens.8
Did the Atlanteans (and in a sense, therefore, the later Egyptians) obtain their zodiac from divine instructors during their third subrace, just as the fifth race did? In view of the fact that Blavatsky also refers to the third root-race in the above quotation, it should be borne in mind that, since the root-races overlap, with each root-race beginning around the midpoint of its predecessor, the third subrace of the Atlanteans would have coincided with one of the later subraces (perhaps the sixth) of the third, Lemurian root-race.9 We are told that during their last two subraces, the Lemurians (or Lemuro-Atlanteans) established the first civilizations under the guidance of their divine instructors, who taught them the arts and sciences, including astronomy.10
(3) The passage may refer to three 180° inversions of the axis rather than three 360° inversions. In the fifth century BCE Herodotus was told by the Egyptian priests that during the past 341 generations, the sun had twice risen where it now sets and twice set where it now rises. This does not necessarily mean that the sun used to rise in the west and set in the east, because as long as the earth rotates on its axis from west to east, as it does at present, the sun will always rise in the east and set in the west, even when the poles are inverted – unless, of course, what we now call the earth’s north pole is renamed the south pole when its inclination exceeds 90°, so that the earth could then be said to rotate from east to west. S.A. Mackey suggests that Herodotus is actually referring to the constellations in which the sun rises and sets: at any given time, the constellations in which the sun rises and sets would be reversed if the earth were to be suddenly inverted.11
Herodotus converts the figure of 341 generations into a period of 11,340 years. However, this is only enough time for the tilt of the axis to change by about 1.7°. Herodotus explains that the figure of 11,340 years is based on a conversion factor of 100 years for every three generations. Curiously, this conversion factor would actually give a period of nearer 11,367 years. Perhaps Herodotus knew more than he was prepared to reveal, and by ‘generation’ he meant a cycle or period with a length of 11,340 years. Multiplying 11,340 by 341 gives a period of 3,866,940 years, during which time the axis would have moved about 597° (3 x 180° = 540°).
This period began not long after the start of the satya-yuga, during the first subrace of the nascent Aryan race. At this time, the axis would have been inclined at an angle of about 100°. It would have been in the plane of the ecliptic when it reached an angle of 270°, and, after returning to 0° (360°), again at 90° and 270°, before reaching its present angle of 336.6° (23.4°). This is in agreement with Blavatsky’s statement (taken from Mackey12) that the Egyptian priests told Herodotus that ‘even since their first Zodiacal records were commenced, the Poles have been three times within the plane of the Ecliptic, as the Initiates taught’.13 This is also sufficient time for the sun to have twice risen where it now sets and twice set where it now rises, in the sense indicated by Mackey.14 In Mackey’s view, the Dendera zodiacs record a period of about 3.5 million years, or three 180° inversions of the poles.
The above speculations are based on the assumption that the inclination of the axis changes at an average rate of 4° every 25,920 years, and no account is taken of the influence of sudden disturbances of the axis, on which no definite information has been given.
Notes
1. H.P. Blavatsky, The Secret Doctrine, TUP, 1977 (1888), 2:353.
2. The Secret Doctrine, 1:650.
3. The Secret Doctrine, 2:436fn.
4. The Secret Doctrine, 2:49.
5. Dialogues of G. de Purucker, TUP, 1948, 1:56, 86.
6. G. de Purucker, Studies in Occult Philosophy, TUP, 1945, pp. 35-9.
7. The Secret Doctrine, 2:368, 433, 435. Blavatsky bases this statement on the work of S.A. Mackey, whose arguments for there being three Virgos in both the circular and rectangular Dendera zodiacs are completely implausible; see Appendix 5, The Dendera zodiacs.
8. The Secret Doctrine, 2:435-6. Blavatsky adds: ‘As the three inversions of the Poles of course changed the face of the zodiac, a new one had to be constructed each time.’
9. Counting a precessional cycle as 25,920 years, this would mean that the third subrace of the Atlanteans, and the sixth (?) subrace of the Lemurians, lived about 6.5 or 7.5 million years ago. But this is difficult to reconcile with the period of about 18.5 million years that is said to have elapsed since the separation of the sexes in the fifth subrace of the third root-race (The Secret Doctrine, 1:150fn; 2:69, 197, 715fn). If 18.5 million years is more or less the correct esoteric figure, the length of subraces in the third and early fourth root-races may have been far longer than 49 precessional cycles, unless a precessional cycle lasted longer in the past due to a slower rate of precession. Note that the current rate of precession averages 1/72° per year, or 1° in 72 years, 72 years being the ‘ideal’ lifetime of a human being in our race and round, and also the average human heart-beat per minute. If humans lived longer in the past (as Blavatsky suggests – H.P. Blavatsky Collected Writings, TPH, 1950-91, 6:117fn), the rate of precession might have been correspondingly slower.
10. The Secret Doctrine, 2:198, 221-2, 316-8.
11. Samson Arnold Mackey, Mythological Astronomy of the Ancients Demonstrated (1822/23), Wizards Bookshelf, 1973, appendix, pp. 11-2.
12. Mythological Astronomy of the Ancients Demonstrated, pp. 2-6. Blavatsky refers to these passages on several occasions: The Secret Doctrine, 2:332, 432, 433, 435, 436.
13. The Secret Doctrine, 2:353.
14. See Appendix 3 for other interpretations of the remarks made by Herodotus.
The Egyptian Temple of Dendera, situated on the west bank of the Nile, is
dedicated to the sky goddess Hathor. It contains two star maps or ‘zodiacs’:
a rectangular one and a circular one. The circular zodiac, about 2.5 metres
in diameter, is a bas-relief carving on two
sandstone blocks, 90 cm thick, which formed part of the ceiling
of a chapel dedicated to Osiris located on the temple roof. It
is a planisphere, a planar projection of many constellations, including
the 12 zodiac constellations. The original carving was blasted from the
ceiling by a French antiquities collector in 1821 and later replaced with
a plaster replica; the original is now on display in the Louvre Museum
in Paris. The rectangular zodiac, also in bas-relief, is found on the ceiling
of the main hypostyle hall; it depicts the zodiac constellations and other
astronomical objects in a sequential fashion. The
two zodiacs have been the subject of great controversy and have been interpreted
in many different ways. They were probably intended to record more than
one important date.
The present temple at Dendera dates from the 1st century BCE, i.e. the late Ptolemaic period, and was completed by the Roman emperor Tiberius (reigned 14-37 CE), who added the portico containing the circular zodiac. However, the temple rests on the foundations of earlier buildings, which – according to an inscription – date back to predynastic times.1

Fig. 1. The ceiling containing the circular zodiac of Dendera, as drawn by Jean-Baptiste Jollois and René Edouard Devilliers (lindahall.org). This drawing is more accurate than the one made by Vivant Denon in 1799, a few months earlier. The vault of heaven is represented by a disk, held up by four priestesses and four pairs of falcon-headed gods. Around the circumference are the 36 decans (star groups near the ecliptic), which were used as a star clock.

Fig. 2. The central part of the circular zodiac. (cartelen.louvre.fr)
The general view is that the constellations of the zodiac depicted in the two Dendera zodiacs are of Babylonian-Greek origin because they are not found in Egypt before it was conquered by Alexander the Great in 332 BCE.2 Although the zodiac constellations generally resemble the Greek/Babylonian forms, some features are Egyptianized. For instance, Aquarius is represented as Hapi, the god of the Nile flood, pouring water from two vases. The constellations do not bear any relation to their actual size in the sky.
There is compelling evidence – though ignored by orthodox scholars – that the ancient Egyptians (or at least the initiates among them) knew of the ‘modern’ zodiac constellations thousands of years before they were supposedly invented and that they also knew of the precession of the equinoxes long before it was (re)discovered by Hipparchos in the 2nd century BCE. The dates and duration of the cults of the bull (Apis) and then the ram (Amun) in dynastic Egypt correspond to the zodiacal ages of Taurus and Aries. The predynastic period was dominated by the twin god and goddess Shu and Tefnut, corresponding to the age of Gemini (the Twins). At that time there was a kingdom of the north (with two capitals) and a kingdom of the south (with two capitals).
In the 5th millennium BCE, the heliacal rising of Sirius took place in Virgo, and Schwaller de Lubicz says that this could explain why Sirius was attributed to Isis and was called ‘the great provider’. In dynastic Egypt the sun was always situated in the constellation Leo on the date of the heliacal rising of Sirius, which marked the beginning of the Nile flood. De Lubicz says that that is why, since the New Kingdom (which began around 1550 BCE), temple gargoyles were carved in the shape of lion heads.3 Robert Bauval has shown that the Egyptians depicted the constellation Leo as a lion from New Kingdom times.4 Moreover, the Sphinx – which is probably tens of thousands of years old – was carved with the body of a lion and the face of a woman, and some have considered it to represent Leo and the adjacent constellation, Virgo.5
After the discovery of the Dendera zodiacs during Napoleon’s campaign in Egypt in the late 1890s, some French scholars suggested that the zodiacs might be 15,000 or more years old – far older than the world itself, according to biblical chronology. Others thought they were no older than 2500 BCE. Champollion, who was then on the verge of deciphering Egyptian hieroglyphics, believed that the circular zodiac had been sculpted during the Ptolemaic era. In 1825 John Bentley argued that the zodiacs were ‘nothing more nor less than the Roman Calendar for the year 708 of Rome [46 BCE], translated into hieroglyphics’.6
The axis of the modern temple is aligned with the heliacal rise of Sirius on 16 July 54 BCE. Other buildings at the site are aligned with the heliacal rise of Sirius some 1200 years earlier, in the time of Ramses II.7 In the 1990s Egyptologist Sylvie Cauville and astrophysicist Éric Aubourg dated the circular zodiac to between June and August 50 BCE, shortly after the start of Cleopatra’s reign, based on the configuration it shows of the five planets, which occurs about once every thousand years. They say that the planets are shown in the constellations where their most recent conjunctions/oppositions occurred before the zodiac was designed. This dating is said to be confirmed by two eclipses recorded on the zodiac: the solar eclipse of 7 March 51 BCE and the lunar eclipse of 25 September 52 BCE. The solar eclipse is represented by a circle containing the goddess Isis holding a baboon by the tail, while the lunar eclipse is represented by an Eye of Horus inside a circle (see fig. 3: the moon (‘lune’) is located below Pisces, and the eye of Horus above it).8

Fig. 3. Circular zodiac of Dendera. The 12 zodiac constellations are shown in green, and the five planets (depicted as gods holding staffs) are shown in blue. The labelling of the constellations is by Aubourg, who admits that some of them are tentative.
R.A. Schwaller de Lubicz argued that the circular zodiac of Dendera
marked three important dates, associated with the last three zodiacal ages (see
fig. 4):9
1. A line drawn perpendicular to the temple’s axis runs between the end
of Aries and the beginning of Pisces, indicating the position of the
equinox in the 1st century BCE, the time of the construction of
the temple and the sculpting of the zodiac. The celestial pole for that time
is located in one of the paws of the jackal, Anubis (Ursa Minor). The ecliptic
pole is located in the breast of the female hippopotamus, Apet (Draco).
2. The true east-west line traverses Aries, indicating the position of the equinox
at the height of the cult of Amun the Ram. This equinoctial
line passes through the two points where circles (of equal radius) drawn around
the celestial and ecliptic poles intersect.10
3. A third equinoctial line, indicated by the hieroglyphs of east and west drawn
on the exterior of the disk, passes between Gemini and Taurus, indicating the
date of the foundation of the empire, the beginning of the cult of the sacred
Bull, Apis, and the adoption of the new calendar, in about 4240 BCE.

Fig. 4. Analysis of the circular zodiac by Schwaller de Lubicz (1998, p. 489).

Fig. 5. The circular zodiac of Dendera (from Bentley, 1825, plate
VIII).
Some of the figures are misdrawn.

Fig. 6. The rectangular zodiac of Dendera (from Bentley, 1825, plate VII). The left and right panels of the zodiac are situated on opposite sides of the hypostyle hall, about 35 metres apart. The lower row of the two panels shows the 36 decans in solar boats. As drawn here, the figures in both the left and right sides of the zodiac are looking towards the feet of the sky goddess Nut. In the actual zodiac, all the zodiacal figures on the right-hand side are facing the head of Nut; in other words, Bentley, like Denon, has reversed their orientation.

Fig. 7. This drawing by Jollois & Devilliers
is more accurate and
shows the figures in the right-hand panel facing in the right direction.
In the early 1800s Charles Dupuis argued that the rectangular zodiac originated
around 13,000 BCE on the assumption that the summer solstice then occurred
in Capricorn (the Goat), which stands at one of the four ends of the zodiac.11
Sampson Arnold Mackey came to a similar conclusion: he held that Capricorn is
found at the ‘top’ of the rectangular zodiac, while Cancer (the
crab/scarab) is divided into two separate figures at the ‘bottom’,
and that this indicated that the winter solstice (when the sun reaches its
lowest point in the sky) then occurred in the 15th degree of Cancer – which
it did just over 16,000 years ago.12
In other words, Mackey identified the ‘top’ of the rectangular zodiac with the head of the sky goddess Nut, and the ‘bottom’ with her feet. However, the Egyptians regarded Nut as arching over the earth with her head and mouth in the west and her genitals and lower body in the east; Nut gave birth to the sun, moon, stars and planets on the eastern horizon and ‘devoured’ them when they reached the western horizon. The scarab (sometimes winged) represented the sun god Khepri (Kheper, Khepera), especially the rising sun being (re)born in the east. One or more scarabs, symbolizing rebirth, are usually depicted near the feet of Nut (and occasionally near its head). On some coffin lids from the Greco-Roman period we see not only scarabs associated with Nut, but also the 12 zodiac constellations, with Cancer represented by a crab.13
 (b)
(b)

Fig. 8. Two details of the rectangular Dendera zodiac: (a) scarab; (b) crab.
Crabs have 10 legs and scarabs have 8. In the circular zodiac Cancer is clearly
represented by a crab. In the left-hand panel of the rectangular zodiac, near
the feet of Nut, there is a scarab (fig. 8a); it has one wing, just like the
solar orbs near the mouth of Nut. Its position matches that of the solar orb
near the feet of Nut in the right-hand panel; both symbolize the rising sun
being born from the ‘lap’/genitals of Nut. The creature in the
right-hand panel just below the solar orb is often said to be a scarab, but
Buchwald & Josefowicz
say it is definitely a crab;14 it
is certainly crab-like in shape and, unlike the scarab, it is facing in roughly
the same direction as the other zodiac constellations in that panel. As can
be seen in fig. 8b, some of its legs are highly stylized and form semicircles.
If each semicircle is interpreted as two legs, then it would be a crab. Since
the rectangular zodiac contains no other representation of Cancer, it seems
that one or both scarab/crab figures must represent it, in addition to any
other symbolic meanings they may have.
It is understandable that Mackey (and others) regarded Cancer as being ‘divided near its middle’, but it is more likely that only the crab designates Cancer; there would then be six zodiac constellations in each panel of the zodiac, with Cancer occupying a unique position. This could be because the zodiac denotes a time when one of the equinoxes or solstices lay in that constellation – and the question is then which equinox or solstice, and in which degree of Cancer did it lie. If, like Mackey, we choose the winter solstice, then the 15th degree of Cancer would represent a time about 16,300 years ago. If we choose the spring equinox, the date represented would be about 9800 years ago, and if we choose the summer solstice, it would be about 3300 years ago. If the equinoctial or solstitial point was just entering Cancer, then these dates would be shifted back about 1080 years.
Another approach focuses on the heliacal rise of Sirius, which marked the beginning of the Egyptian year (which was celebrated at Dendera) and the beginning of the Nile flood, an event vital to the livelihood of ancient Egypt. It approximately coincided with the summer solstice throughout dynastic Egyptian history, occurring in Leo until around 500 BCE, when it moved into Cancer.15 In the rectangular zodiac (see fig. 9), next to the head of Hathor (beneath the solar orb near the crab) we see in the upper panel a figure pouring water from both hands (usually taken to represent the Nile flood), and a recumbent cow with a star between its horns, representing Sirius. In the lower panel, next to the solar orb, we see a small boat carrying a lotus flower from which emerges a snake. The snake symbolizes the rising sun on the first day of the New Year, the lotus flower being the first object that appeared on the primordial sea on the first day of the world creation.

Fig. 9. Part of the rectangular zodiac.
Mackey believed that the Dendera zodiacs also represented an antiquity far greater than 16,000 years, but
his arguments are unconvincing.16 He
held that the rectangular zodiac represents the earth’s poles in the
plane of the ecliptic (i.e. a tilt of 90°), which last occurred over 400,000
years ago, and that the circular zodiac represents the earth’s poles
coinciding with the ecliptic poles (i.e. a tilt of 180° or 0°),
which last occurred over 540,000 years earlier, when the earth’s axis
was inverted. He also says that the zodiacs have features indicating that
these positions of the poles had been repeated three times – a reference
to the depictions of Leo and Virgo. The zodiacs therefore represented an
antiquity of some 3.5 million years, during which time the earth’s
poles had been ‘three times within the plane of the ecliptic’. It is
interesting to note that, as well as referring to Mackey as the Oedipus who
had understood the riddle of the zodiacs, H.P. Blavatsky also commented: ‘On
the Dendera Zodiac as preserved by the modern Egyptian Coptic and Greek adepts,
and explained a little differently by Mackey ...’17

Fig. 10. Another part of the (cleaned) ceiling of the main hypostyle hall in the Temple of Hathor. (en.wikipedia.org)
The lion representing Leo is clearly visible in both the circular and rectangular
zodiacs (fig. 5, no. 46, and fig. 6, no. 61). Mackey (like Bentley) believed
that the circular zodiac contains a second Leo, i.e. the lionlike creature
with a protruding tongue (no. 65 in fig. 5, but depicted more accurately in
fig. 3); the fact that its tail is turned up over its
back rather than curving downwards indicates according to Mackey that the Lion
(and every other constellation) had become inverted. This lionlike creature,
and the two figures on either side of it, are nowadays associated with the
constellations Centaurus and Lupus (see fig. 3), which matches their positions
below Libra and Virgo.18
Mackey writes that in the rectangular zodiac ‘we see three Virgins between the Lion and the Scales; the last of which holds, in her hand, an ear of wheat’. The figure of Virgo holding an ear of wheat is clearly recognizable. But where are the other two Virgos that Mackey refers to? Fig. 11, part of Mackey’s own drawing of the rectangular zodiac, clearly shows what he had in mind.19

Fig. 11. Mackey’s three Virgins.
Mackey is wrong to believe that the two female figures with a star
over their heads (fig. 6, nos. 65 and 66) standing directly to the right
of the Virgo holding a wheat ear (no. 67) are also Virgos. A total
of 24 such figures can be seen in the rectangular zodiac,
usually beside a tablet (nos. 1, 10, 11, 15, 19, 26, 27, 34,
35, 43, 45, 49, 59, 65, 66, 72, 73, 78, 79, 88, 89, 93, 99, 102; some of them
are misdrawn in fig. 6).
They represent the 24 hours of
the day and night, and are a common feature of ancient Egyptian astronomical
art, especially that dating from the Greco-Roman period.
According to Mackey, in the circular zodiac, too, ‘there are three virgins, which represent the three Decans, into which each sign of the Zodiac was divided. But, here, the first virgin is represented with a Child on her knee ...’20 The female figure holding a child (which is almost certainly not meant to represent Virgo21) and the Virgo holding a wheat stalk are clearly recognizable (nos. 53 and 56 in fig. 5). But where is the third Virgo? Fig. 12 is Mackey’s own drawing of the circular zodiac.22 The figure holding a scythe (fig. 5, no. 59), standing between the female figure with a child and the Lion is said by Mackey to represent Boötes, so the only remaining candidate for the third Virgin is the figure to the left of the Virgin holding a wheat ear (fig. 5, no. 60). But it is an odd-looking Virgin: the loincloth indicates that it is a male, it has an animal head, and Egyptologists identify it as Saturn (‘Horus the Bull’).23

Fig. 12. Three more Virgins?
In the circular zodiac, Leo is represented standing on a snake
(fig. 5, no. 46); behind it is a woman standing on and holding
its tail, who has sometimes been interpreted as (a second) Virgo,24 and there is also a bird standing on the snake. In fig. 5 (no. 47) the woman is misdrawn by Bentley as an animal, while in fig. 3 she is drawn correctly (see fig. 13). Bentley’s drawing is based on the drawing in volume 2 of D.V. Denon’s Voyage dans la Basse et la Haute Egypte (1802). Since Mackey based his interpretation of the circular zodiac on Denon’s depiction of it, in which the figure to the left of Leo is misdrawn, he does not include it in his own drawing of the circular zodiac (fig. 12), though it would make a better candidate for another Virgo.

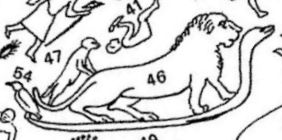
Fig. 13. Above: Details of the circular zodiac as drawn by Denton (left) and Bentley (right, from fig. 5).
Below: A more accurate rendering (from fig. 3).

In the rectangular zodiac, too, Leo is shown
standing on a snake (fig. 6, no. 61), and behind it (in the damaged part) there is a woman holding the Lion’s tail in one
hand and a flail in the other, and also a bird; behind this woman there seems to be another figure. These figures are barely visible
in fig. 6, but are more clearly visible in the photos in fig. 14. The snake represents Hydra (as Mackey rightly says) and the bird represents Corvus (Raven/Crow); both these
constellations were recognized by the Babylonians, Greeks and Romans. As with the circular zodiac, Mackey also omits
the female figure standing directly behind Leo in his drawing of the rectangular zodiac
(fig. 11), as his drawing is based on Denon’s drawing, in which the figure is barely visible.


Fig. 14. Photographs of Leo in the rectangular zodiac.
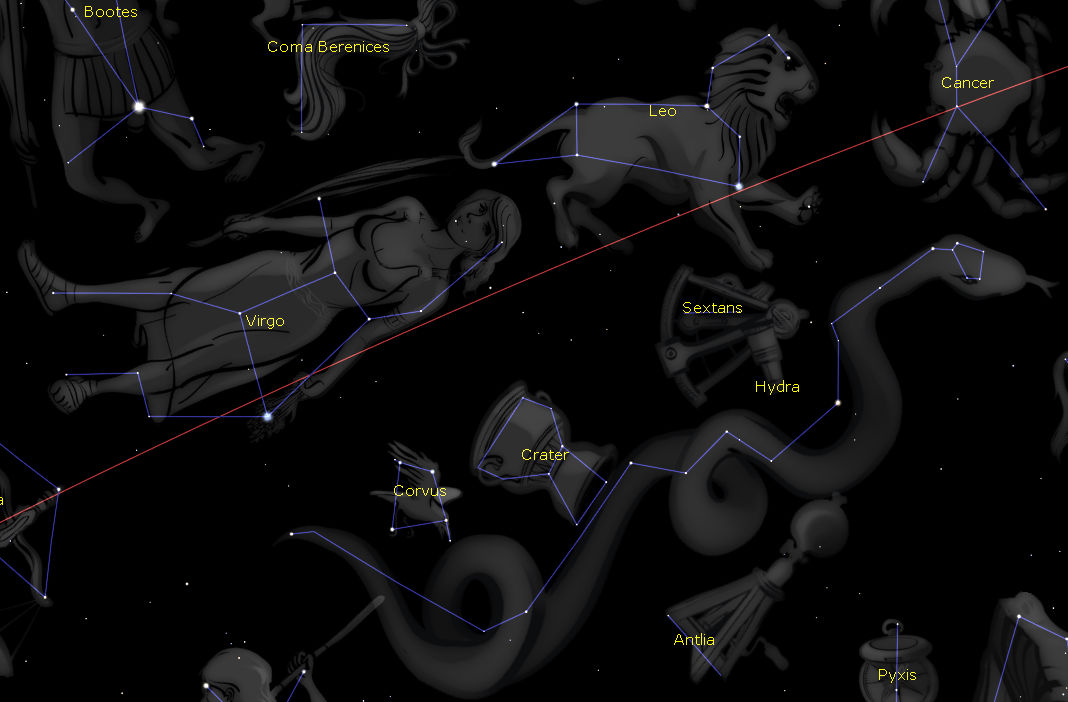
Fig. 15. Virgo, Leo, Coma Berenices, Hydra, Corvus, ecliptic (red).
The modern Virgo constellation, which extends along the ecliptic for over
40°, is a combination of the Babylonian Furrow and Frond, the eastern and
western sectors of Virgo. In the circular Dendera zodiac the Virgo figure holding
the ear of wheat corresponds to the Furrow (or barley goddess), and the female
figure standing behind the Lion corresponds to the Frond of Erua, whose constellation
was located among the stars of Coma Berenices and the western half of Virgo.
A late Babylonian text describes her as a goddess holding a frond of the date
palm in her right hand, but a Neoassyrian text describes her as holding a whip
which ‘points towards the Lion’s
tail’.25
(a) They represent three precessional cycles:
‘Isis-Osiris’ reigned in Egypt before the Dendera Zodiac was painted on the ceiling of that temple, and that is over 75,000 years ago!27
since the Dendera Zodiac shows the passage of three sidereal years, the great Pyramid must have been built 78,000 years ago ...28
the Egyptians have on their Zodiacs irrefutable proofs of records having embraced more than three-and-a-half sidereal years – or about 87,000 years ...29
(b) They represent three 180° inversions of the axis:
the Dendera zodiac ..., with its mysterious three Virgos between the Lion and Libra, has found its Oedipus [Mackey], who understood the riddle of these signs, and justified the truthfulness of those priests who told Herodotus that ... even since their first Zodiacal records were commenced, the Poles have been three times within the plane of the Ecliptic.30
(c) They represent three 360° inversions of the axis:
The three ‘Virgins,’ or Virgo in three different positions, meant, with both, the record of the first three ‘divine or astronomical Dynasties,’ who taught the third root-race; and after having abandoned the Atlanteans to their doom, returned (or redescended, rather) during the third sub-race of the fifth, in order to reveal to saved humanity the mysteries of their birth-place – the sidereal Heavens.31
Further details of the last two interpretations can be found in Appendix 4.
In addition to Cancer, Leo and Virgo, there have been claims that several other constellations appear more than once in the Dendera zodiacs, but none is very convincing.
In the circular zodiac (fig. 5), Gemini is represented by no. 35, and according to Bentley also by no. 82.32 However, if we look at figures 2 and 3 we can see that there is only one person depicted, not two (identified as Cygnus/Lyra in fig. 3). This is a serious blunder by Bentley.
Aries is represented in the circular zodiac (fig. 5) by no. 25, but there is also a small bovine creature seated on the underside of the Bull’s Foreleg/Thigh (the Plough or Big Dipper, i.e. the seven brightest stars of Ursa Major) (no. 36), with its head turned back. Some researchers have called it a ‘crouching lion’ and say that it is part of Egypt’s indigenous northern group of constellations, but Robert Bauval says that the creature ‘is very similar to the Aries/Ram figure shown on the various Ptolemaic zodiacs i.e. it has bovine forelegs depicted as the Aries/Ram of Denderah, and its head is turned in the same posture looking backwards’ (see fig. 16).33 Gavin White argues that the animal is a sheep and corresponds to the Babylonian Ewe, which probably stood for a single star located on the shaft of the Babylonian Wagon (Ursa Major).34

Fig. 16. Photograph by Richard Fusniak of a marble reproduction from a plaster
cast of the original circular zodiac (Fitzwilliam museum, Cambridge, England).
One of the reasons why some French researchers in the early 19th century
thought the zodiacs could be 15,000 years old, is that certain constellations
were repeated at an interval of about six signs.35 For
example, in the circular zodiac (fig. 5), Aquarius is represented by no.
10, and allegedly by no. 50 as well, while in the rectangular zodiac (fig.
6) it is represented by no. 12 and allegedly by no. 56 too. The
two alleged extra figures of Aquarius are shown in fig. 17 below. In the
circular zodiac the figure is an enthroned goddess holding aloft a pair of
vases (with no water emerging from them); the same goddess, wearing the same
distinctive headdress, appears in the rectangular zodiac, but with streams
of water flowing from her vases. Gavin White argues that these figures represent
the Babylonian Star of Eridu, located in the region now occupied by the stern
of the Argo; the rising of the star heralded the end of the summer drought
and the start of the autumn rainy season.36


Fig. 17. Details from the circular and rectangular zodiacs.
As for the rectangle containing wavy lines (fig. 5, no. 64) under the paws
of the Lion/Lupus/Centaurus (no. 65), Bentley interprets it as Pisces and
Mackey as Aquarius,37 Gavin White says the zigzag lines represent
irrigation channels filled with water, and that it is the Babylonian
symbol of the Abyss, the subterranean freshwater reservoir, which was the
dwelling place of Enki (the god of wisdom), various mythical creatures, and
the seven sages who brought the gifts of civilization to mankind before the
great flood. The Abyss symbol under the feet of the lionlike creature
in the circular zodiac probably stands for Crux, the Southern Cross, whose
stars approximately form a square. The Abyss symbol also appears in the Pisces
constellation (fig. 5, no. 18), where it represents the four bright stars that form the Square
of Pegasus, known in Babylonian astronomy as the Field. White says that the
Abyss symbol was used for the stars of Crux, because they mark the start
of the rainy season and the rise in river levels, and it was used for the
Square of Pegasus because these stars marked the start of the main flooding
season and the time when crops received the final irrigation.38
Notes
1. John Anthony West, Serpent in the Sky: The high wisdom of ancient Egypt, Quest, 1993, pp. 100-1.
2. Gavin White notes various close
correspondences between the Dendera constellations and what we know of the
Babylonian constellations. He believes that the Babylonians began to organize
stars into constellations in the 5th millennium BCE, and that in the mid-3rd
millennium BCE about half the archaic constellations were replaced by new
star figures due to the changes brought about by the precession of the equinoxes
(Gavin White, Babylonian Star-Lore: An illustrated guide to the star-lore
and constellations of ancient Babylonia, Solaria Publications, 2nd ed.,
2008; A new interpretation of the Dendera Zodiac, 2007, solariapublications.com).
Gary Thompson argues that there is no concrete evidence
of any knowledge of the zodiac in Egypt until the Greek/Ptolemaic period; that
the cuneiform evidence shows that the 12-constellation zodiac was invented by
the Babylonians in the first millennium (circa 750 to 450 BCE); and that there
is no evidence that the Babylonians adopted the zodiac from elsewhere (Critique
of Alexander Gurshtein’s theory of constellation development, Sep.
2012, members.westnet.com.au).
3. R.A. Schwaller de Lubicz, Sacred Science: The king of Pharaonic theocracy (1961), Inner Traditions, 1982, pp. 117-9, 176-7; R.A. Schwaller de Lubicz, The Temple of Man, Inner Traditions, 1998, vol. 1, pp. 486-90; West, Serpent in the Sky, pp. 98-100.
4. Robert Bauval, ‘The Lion (Leo) was known in the New Kingdom’, 2002, robertbauval.co.uk.
5. R.H. Allen writes: ‘... Pliny is authority for the statement that the Egyptians worshipped the stars of Leo because the rise of their great river was coincident with the sun’s entrance among them. For the same reason the great Androsphinx is said to have been sculptured with Leo’s body and the head of the adjacent Virgo; although Egyptologists maintain that this head represented one of the early kings, or the god Harmachis. Distinct reference is made to Leo in an inscription on the walls of the Ramesseum at Thebes, which, like the Nile temples generally, was adorned with the animal’s bristles ...’ (Star Names: Their lore and meaning (1899), Dover, 1963, p. 253, constellationsofwords.com). The rectangular zodiac in the temple of Esna (see note 15 below) shows a sphinx with a lion’s body and a woman’s head. On the age of the Sphinx, see: Mysteries of the Great Pyramid, davidpratt.info.
6. J. Bentley, A Historical View of Hindu Astronomy (1825), Como Publications, 1981, pp. 251-82. Blavatsky writes: ‘Europeans are unacquainted with the real Zodiacs of India, nor do they understand those they happen to know (witness Bentley)’ (H.P. Blavatsky, The Secret Doctrine, TUP, 1977 (1888), 2:431).
7. Sylvie Cauville, ‘Le temple d’Isis à Dendera’, Bulletin de la Société Française d’Egyptologie, no. 123, 1992, pp. 31-48, sfe-egyptologie.fr.
8. Éric Aubourg, ‘La date
de conception du temple d’Hathor à Dendera’, Bulletin
de l’Institut Français d’Archéologie, no.
95, 1995, pp. 1-10, ifao.egnet.net;
Jo Marchant, ‘Decoding the ancient Egyptians’ stone sky map’, New
Scientist, 5 July 2010, newscientist.com.
Cauville and Aubourg explicitly reject the idea that
the positions of the planets are purely symbolic. But Gary D. Thompson comments
that they ‘appear to be unaware of the fact that the planets on the planisphere
are located in their so-called exaltation points (“hypsomata”), i.e.,
the signs in which they are assumed to have special powers. This is a well known
tradition in Late-Babylonian and Hellenistic astrology’ (Late Egyptian
constellations: Denderah zodiac, Sep. 2010, members.westnet.com.au).
9. De Lubicz, Sacred Science, pp. 283-6; The Temple of Man, vol. 1, pp. 486-90; West, Serpent in the Sky, pp. 100-2; Peter Tompkins, Secrets of the Great Pyramid, Harper & Row, 1978, pp. 169-75.
10. Note that the positioning of Libra and especially Cancer is anomalous (see fig. 4). Cancer could be regarded as the inner point of an irregular spiral.
11. Jed Z. Buchwald & Diane Greco Josefowicz, The Zodiac of Paris: How an improbable controversy over an ancient Egyptian artifact provoked a modern debate between religion and science, Princeton University Press, 2010, p. 113. Another possibility is that instead of Capricorn being the constellation in which the solstice sun rose, it is the constellation in which it set; this would bring the date forward by about 10,500 years (p. 208).
12. Samson Arnold Mackey, The Two Zodiacs of Tentyra, and the Zodiac of Thebes, Norwich, 1932, pp. 15-7.
13. Antonios Goyios, S.A. Mackey and the Dendera zodiacs, Oct. 2009, blavatskyarchives.com. Schwaller de Lubicz says that Cancer is represented by a scarab in the tomb of Ramesses VI (The Temple of Man, vol. 1, p. 483).
14. Buchwald & Josefowicz, The Zodiac of Paris, p. 365.
15. The Zodiac of Paris, pp. 141-2, 196-7. Some
researchers have seen Leo as the ‘first’ zodiac constellation in the rectangular
zodiac, rather than Cancer. E.g. in the early 1800s Jean-Baptiste Caraboeuf
(and others) held that the rectangular Dendera zodiac showed the summer solstice
in Leo (approaching Cancer) and that it might date as far back as the middle
of the 3rd millennium BCE, while the rectangular zodiac in the temple of Esna
showed the summer solstice occurring in Virgo and therefore dated back no later
than the end of the 5th millennium BCE, and perhaps a thousand or more years
before that. It was recognized that the Dendera zodiac might have been made
in Grecian times but still refer back to much older periods (pp. 104,
109, 163-4).
Joseph Fourier interpreted the rectangular
zodiac to mean that the heliacal rise of Sirius occurred at the boundary between
Leo and Cancer, which he dated to 2100 BCE, and he believed that the zodiac
in the temple of Esna originated in 2500 BCE, when the heliacal rise still
took place unambiguously in Leo. These dates are correct if we consider
the true heliacal rise, but not if we consider what was visible from
the ground,
which requires taking account of atmospheric refraction; this would shift
these dates forward by around 1500 years (pp. 196-200).
The zodiac in the Temple of Esna is shown
below (revisedhistory.org).

16. Samson Arnold Mackey, Mythological Astronomy of the Ancients Demonstrated (1822/23), Wizards Bookshelf, 1973, pp. 2-6; The Two Zodiacs of Tentyra, and the Zodiac of Thebes, pp. 15-21; S.A. Mackey, The Original Design of the Ancient Zodiacal and Extra-Zodiacal Constellations, Norwich, 1834, pp. 21-2. The relevant quotations can be found in Appendix 6.
17. The Secret Doctrine,
2:368, 432. Blavatsky makes the following comment on Mackey’s
view that the myth of the gods ascending and descending referred to the movement
of the zodiac constellations at a time when the earth’s poles were
in the plane of the ecliptic: ‘This is an ingenious
explanation, even if it is not altogether free from occult heresy’ (SD
2:357).
Mackey’s scattered comments on the
Dendera zodiacs are sometimes rather
dubious, if not plain wrong. His assertion that in the circular zodiac the zodiac
constellations are in the plane of the equator, and the pole of the earth and
the pole of the ecliptic coincide, receives no support from Schwaller de Lubicz’s
analysis.
18. Robert Bauval writes: ‘This “crouching
lion” on the Denderah Zodiac, being under LIBRA, is probably a proto-representation
of the classical “Centaur” figure’ (‘The Lion (Leo)
was known in the New Kingdom’, 2002, robertbauval.co.uk).
The
figure in the zodiac certainly looks more like a lion than a wolf (Lupus) or
a centaur, but Lupus was not recognized as a wolf until about the 16th century.
The ancient Greeks called this constellation Therion, representing an unspecified
wild animal, while the Romans called it Bestia, the Beast. It was visualized
as impaled on a long pole held by the adjoining constellation of Centaurus,
the Centaur, who was holding it toward the constellation Ara (the Altar)
as though he were about to sacrifice it. The Greek astronomer Hipparchos renamed
some of the stars Therion in the 2nd century BCE, while Ptolemy first gave
them the name Lupus in the 2nd century CE (ianridpath.com;
topastronomer.com).
The Arabs also called Lupus Al Asadah, the Lioness. The Greek constellation
is thought to be based on the Babylonian figure known as the Mad Dog,
a hybrid creature that combined the head and torso of a man with the legs and
tail of a lion (constellationsofwords.com).
Gavin White argues that the lionlike creature
corresponds to the Babylonian Wild Boar constellation, located among the stars
of Centaurus. He argues that the protruding tongue of the Dendera animal is a
misunderstanding of the Boar’s tusks and that its mane is a misrepresentation
of the Boar’s
spinal brush. He believes that the hippo-man wearing the white crown of Upper
Egypt standing behind the lionlike creature corresponds to the position of the
Mad Dog constellation, located among the stars of Lupus. He notes that the Boar
was said to be located close to the Abyss, and we see the symbol for the Abyss
(a rectangle filled with wavy lines) beneath the feet of the Dendera figure.
The bull-headed
man holding a hoe-like implement standing in front of the Abyss symbol probably
represents the Babylonian Harrow constellation, located among the western
stars of Centaurus (Babylonian
Star-Lore,
pp. 57-60, 126-7, 145-6, 226-8; A new interpretation of the Dendera
Zodiac).
19. Mythological Astronomy, p. 4; The Two Zodiacs of Tentyra, and the Zodiac of Thebes, plate A. In The Original Design of the Ancient Zodiacal and Extra-Zodiacal Constellations, Mackey writes: ‘[The] virgin is thrice repeated in the long Zodiac of Dendera, one of which holds up a wheat-ear between Leo and the Balance or Scales’ (p. 21).
20. The Original Design of the Ancient Zodiacal and Extra-Zodiacal Constellations, pp. 21-2. In The Two Zodiacs of Tentyra, he states that in the circular zodiac ‘Virgo is intermixed with Leo, and the first of the three virgins has her child on her lap’ (p. 20).
21. Bentley interpreted the enthroned goddess holding a child as Isis holding Horus (A Historical View of Hindu Astronomy, p. 276), but Schwaller de Lubicz, like Mackey, took it to represent Virgo (The Temple of Man, vol. 2, p. 776fn). Gavin White argues that the figure corresponds to the Babylonian Ninmah, the Exalted Lady, a goddess associated with motherhood and children, whose constellation was located in the southern skies below the Serpent and Lion (among the easternmost stars of Argo), which matches its position on the Dendera star map (Babylonian Star-Lore, pp. 147, 245).
22. The Two Zodiacs of Tentyra, and the Zodiac of Thebes, plate B.
23. Goyios, S.A. Mackey and the Dendera zodiacs; Mackey, The Two Zodiacs of Tentyra, p. 20; The Original Design of the Ancient Zodiacal and Extra-Zodiacal Constellations, p. 21.
24. Thompson, Late Egyptian constellations: Denderah zodiac: ‘Also, the female figure standing on the Lion’s tail, which she grasps with her hand, has been interpreted by some as representing Virgo.’ Schwaller de Lubicz regarded the female figure as an integral part of the symbol for Leo (Temple of Man, p. 483). However, not all Egyptian representations of Leo include this figure. A small female figure standing immediately behind Leo also appears in the Esna zodiac (see note 15), in addition to Virgo (holding the tail of the Sphinx in the lower panel).
25. White, Babylonian Star-Lore, pp. 112-8, 243.
26. The Secret Doctrine, 2:433; see also 2:368, 435. Blavatsky states: ‘Having seen [the Dendera zodiacs] personally, the writer has no longer need to trust to what other students – who have examined and studied both very carefully – have to say of them’ (2:431).
27. The Secret Doctrine, 2:374fn.
28. The Secret Doctrine, 2:432.
29. The Secret Doctrine, 2:332; see Mysteries of the Great Pyramid, davidpratt.info.
30. The Secret Doctrine, 2:368.
31. The Secret Doctrine, 2:435-6.
32. Bentley, A Historical View of Hindu Astronomy, p. 279.
33. robertbauval.co.uk; See also Robert M. Schoch and Robert Bauval, Origins of the Sphinx: Celestial guardian of pre-Pharaonic civilization, Rochester, VE: Inner Traditions, 2017, pp. 318-27. It is also identified as a ram by Giorgio de Santillana & Hertha von Dechend, Hamlet’s Mill: An essay investigating the origins of human knowledge and its transmission through myth, Nonpareil Books, 1969, p. 405. Thompson (Late Egyptian constellations: Denderah zodiac) calls it a crouching lion.
34. White, Babylonian Star-Lore, p. 101.
35. See Bentley, A Historical View of Hindu Astronomy, pp. 251-2.
36. Babylonian Star-Lore, pp. 98-100, 244-5.
37. Bentley, A Historical View of Hindu Astronomy, p. 277; Mackey, The Two Zodiacs of Tentyra, p. 20.
38. Babylonian Star-Lore, pp. 103-7, 169, 245.
Sampson Arnold Mackey (1765-1843) lived for most of his adult life in Norwich,
where he worked as a shoemaker. He received minimal education, but pursued
his own studies of astronomy, geology and mythology. He gave lectures on
his theories, and published several books and pamphlets at his own expense.
He was one of the first writers to publicly challenge the biblical dogma
that the earth was no more than about 6000 years old, and argued instead
that the earth, and humanity too, was millions of years old. He was
invited to join the Freemasons, but refused to do so as he wanted to preserve
his independence. He died in an almshouse.
For further information on Mackey’s life and work, see Blavatsky Collected Writings, 14:545-9, and two books by Joscelyn Godwin: Arktos: The polar myth in science, symbolism, and Nazi survival, Phanes Press, 1993, pp. 196-202, and The Theosophical Enlightenment, State University of New York Press, 1994, pp. 67-76.
Godwin makes the following criticism:
Like many an autodidact, Mackey hurt his case by riding his hobby-horse to the limit. Every myth or legend he came across seemed to illustrate the experiences of mankind under the changing conditions of the shifting axis. All solar myths referred to the apparent behavior of the sun; serpent myths, to the spiral path of the pole. The different volves of the spiral were always mythologized as intelligent beings, which explained away all the stories of the gods and their progeny. All numbers in theogony and myth referred to celestial mathematics, which Mackey believed to have been fully understood by the priest-astronomers of antiquity. (The Theosophical Enlightenment, p. 71)
Although Mackey may have overstated his case, H.P. Blavatsky clearly considered some of his views worthy of quotation. All the passages in Blavatsky’s works which quote from or draw on Mackey’s writings are reproduced below, and the page numbers of the relevant passages in Mythological Astronomy of the Ancients Demonstrated [MA] are indicated. The relevant passages from MA are then given. Finally a few additional passages referring to the Dendera zodiacs are given from several of Mackey’s works. For a critical appraisal of Mackey’s views on the Dendera zodiacs, see Appendix 5 and also Antonios Goyios, S.A. Mackey and the Dendera zodiacs, Oct. 2009, blavatskyarchives.com.
H.P. Blavatsky
SD 1:654-5
‘Christian theologians think it their duty to write against the long periods of Hindu chronology,’ argues very pertinently S.A. Mackey, the Norwich ‘philosopher, astronomer, and shoemaker.’ ‘But when a man of learning crucifies the names and numbers of the ancients, and wrings and twists them into a form which means something quite foreign to the intention of the ancient authors; but which, so mutilated, fits in with the birth of some maggot pre-existing in his own brain with so much exactness that he pretends to be amazed at the discovery, I cannot think him quite so pardonable’ (Key of Urania). [MA, part 2, 23-4]
This is intended to apply to Captain (late Colonel) Wilford, but the words may fit more than one of our modern Orientalists.
SD 2:331
Every sidereal year the tropics recede from the pole four degrees in each revolution from the equinoctial points, as the equator rounds through the Zodiacal constellations. Now, as every astronomer knows, at present the tropic is only twenty-three degrees and a fraction less than half a degree from the equator. Hence it has still 2½ degrees to run before the end of the Sidereal year; which gives humanity in general, and our civilized races in particular, a reprieve of about 16,000 years. [MA, app., 25-6]
See part 3, section 4 of this article.
SD 2:332
The Egyptian priests assured Herodotus that the Pole of the Earth and the Pole of the Ecliptic had formerly coincided [MA, 2]. But, as remarked by the author of the Sphinxiad [the Sphinxiad is actually a zodiacal drawing in MA], ‘These poor benighted Hindoos have registered a knowledge of Astronomy for ten times 25,000 years since the (last local) Flood (in Asia), or Age of Horror,’ in the latitude of India [MA, app., 23]. And they possess recorded observations from the date of the first Great Flood within the Aryan historical memory – that which submerged the last portions of Atlantis, 850,000 years ago.
SD 2:356
... every occultist knows that the Serpent alluded to is the north pole, as also the pole of the heavens.* The latter produces the seasons according to the angle at which it penetrates the centre of the earth. [MA, 39]
*Symbolized by the Egyptians under the form of a Serpent with a hawk’s head.
SD 2:357-8
The Egyptians, according to Eusebius, who for once (and for a wonder) wrote the truth, symbolized kosmos by a large fiery circle, representing a serpent with a hawk’s head lying across its diameter. ‘Here we have the pole of the earth within the plane of the ecliptic, attended with all the fiery consequences that must arise from such a state of the heavens: when the whole Zodiac in 25,000 (odd) years, must have reddened with the solar blaze, and each sign must have been vertical to the polar region.’ (see Mackey’s ‘Sphinxiad’.) [MA, 42]
Meru – the abode of the gods – was placed, as before explained, in the North Pole, while Pātāla, the nether region, was supposed to lie in the South. As each symbol in esoteric philosophy has seven keys, geographically, Meru and Pātāla have one significance and represent localities; while astronomically, they have another, and mean ‘the two poles,’ which meaning ended by their being often rendered in exoteric sectarianism – the ‘Mountain’ and the ‘Pit,’ or Heaven and Hell. ... As the author just quoted half explains, Helion and Acheron meant nearly the same: ‘Heli-on is the Sun in the highest’ (Helios, Heli-on, the ‘most high’); ‘and Acheron is 32 deg. above the pole, and 32 below it, the allegorical river being thus supposed to touch the northern horizon in the latitude of 32 degrees. The vast concave, that is for ever hidden from our sight and which surrounded the southern pole, being therefore called the PIT, while observing, toward the Northern pole that a certain circuit in the heavens always appeared above the horizon – they called it the Mountain. As Meru is the high abode of the Gods, these were said to ascend and descend periodically; by which (astronomically) the Zodiacal gods were meant, the passing of the original North Pole of the Earth to the South Pole of the heaven.’ ‘In that age,’ adds the author of that curious work, the ‘Sphinxiad’ and of ‘Urania’s Key to the Revelations’ – ‘at noon, the ecliptic would be parallel with the meridian, and part of the Zodiac would descend from the North Pole to the north horizon; crossing the eight coils of the serpent (eight sidereal years, or over 200,000 solar years), which would seem like an imaginary ladder with eight staves reaching from the earth up to the pole, i.e., the throne of Jove. Up this ladder, then, the Gods, i.e., the signs of the Zodiac, ascended and descended. (Jacob’s ladder and the angels) ... It is more than 400,000 years since the Zodiac formed the sides of this ladder.’ [MA, 41, 44, 46-7] . ...
This is an ingenious explanation, even if it is not altogether free from occult heresy. Yet it is nearer the truth than many of a more scientific and especially theological character.
SD 2:360
[T]he two figures in white and black stone have existed in the temples of Egypt from time immemorial – agreeably to tradition; and historically – ever since the day of King Cambyses, who personally saw them. ... These figures were the two Kabiri personifying the opposite poles. Herodotus (Thalia, No. 77) tells posterity that when Cambyses entered the temple of the Kabirim, he went into an inextinguishable fit of laughter, on perceiving what he thought a man erect and a woman standing on the top of her head before him. These were the poles, however, whose symbol was intended to commemorate ‘the passing of the original North Pole of the Earth to the South Pole of the Heaven,’ as perceived by Mackey.* [MA, 40-1] But they represented also the poles inverted, in consequence of the great inclination of the axis, bringing each time as a result of the displacement of the Oceans, the submersion of the polar lands, and the consequent upheaval of new continents in the equatorial regions, and vice versâ. These Kabirim were the ‘Deluge’ gods.
*Who adds that the Egyptians had various ways of representing the angles of the Poles. Also in Perry’s View of the Levant there is ‘a figure representing the South Pole of the Earth in the constellation of the Harp,’ in which the poles appear like two straight rods, surmounted with hawks’ wings, but they were also often represented as serpents with heads of hawks, one at each end. [MA, 41]
SD 2:362fn
It is a curious idea – yet one not very far from the truth, perhaps – that speculation of Mackey, the self-made Adept of Norwich, found in his ‘Mythological Astronomy.’ He says that the Kabiri named Axieros and Axiokersa derived their names (a) from Kab or Cab, a measure, and from Urim, the heavens: the Kabirim being thus ‘a measure of the heavens;’ and (b) that their distinctive names, implying the principle of generation, referred to the sexes. For, ‘the word sex was formerly understood by aix; which has now settled ... into sex.’ And he refers to ‘Encyclopaedia Londinus’ at the word ‘aspiration.’ Now if we give the aspirated sound to Axieros, it would be Saxieros; and the other pole would be Saxiokersa. The two poles would thus become the generators of the other powers of nature – they would be the parents: therefore the most powerful gods. [MA, 38-9]
SD 2:368
Africa, as a continent, it is said, appeared before Europe did; nevertheless it appeared later than Lemuria and even the earliest Atlantis. That the whole region of what is now Egypt and the deserts was once upon a time covered with the sea, was known firstly through Herodotus, Strabo, Pliny, and all the Greeks; and, secondly, through geology. Abyssinia was once upon a time an island; and the Delta was the first country occupied by the pioneer emigrants who came with their gods from the North-east.
When was it? History is silent upon the subject. Fortunately we have the Dendera Zodiac, the planisphere on the ceiling of one of the oldest Egyptian temples, which records the fact. This Zodiac, with its mysterious three Virgos between the Lion and Libra, has found its Oedipus, who understood the riddle of these signs, and justified the truthfulness of those priests who told Herodotus that:– (a) The poles of the Earth and the Ecliptic had formerly coincided; and (b) That even since their first Zodiacal records were commenced, the Poles have been three times within the plane of the Ecliptic, as the Initiates taught. [MA, 2, 4]
SD 2:406-8
Surely, if the Hindu Purānas give a description of wars on continents and islands situated beyond Western Africa in the Atlantic Ocean; if their writers speak of Barbaras and other people such as Arabs – they who were never known to navigate, or cross the Kala pani (the black waters of the Ocean) in the days of Phoenician navigation – then their Puranas must be older than those Phoenicians (placed at from 2,000 to 3,000 years B.C.). At any rate those traditions must have been older; as –
‘In the above accounts,’ writes an adept, ‘the Hindus speak of this island as existing and in great power; it must, therefore, have been more than eleven thousand years ago.’ [MA, part 2, 70]
But another calculation and proof may be adduced of the great antiquity of these Hindu Aryans who knew of (because they had once dwelt in it) and described the last surviving island of Atlantis – or rather of that remnant of the Eastern portion of that continent which had perished soon after the upheaval of the two Americas – the two Varshas of Pushkara. This may be demonstrated, moreover, on an astronomical calculation by an adept who criticises Wilford. For re-calling what the Orientalist had brought forward concerning the Mount Ashburj ‘at the foot of which the sun sets,’ where was the war between the Devatas and the Daityas, he says:–
‘We will consider, then, the latitude and longitude of the lost island, and of the remaining Mount Ashburj. It was on the seventh stage of the world, i.e., in the seventh climate (which is between the latitude of 24 degrees and latitude 28 degrees north). ... This island, the daughter of the Ocean, is frequently described as lying in the West; and the sun is represented as setting at the foot of its mountain (Ashburj, Atlas, Teneriffe or Nila, no matter the name), and fighting the white Devil of the “White Island.” ’ [MA, part 2, 69] ...
It was just remarked that since, in the Purānic accounts, the island is still existing, then those accounts must be older than the 11,000 years elapsed since Sancha dwipa, or the Poseidonis of Atlantis, disappeared. Is it not barely possible that Hindus should have known the island still earlier? Let us turn again to astronomical demonstrations, which make this quite plain if one assumes, according to the said adept, that ‘at the time when the summer tropical “colure” passed through the Pleiades, when cor-Leonis [Regulus] would be upon the equator; and when Leo was vertical to Ceylon at sunset, then would Taurus be vertical to the island of Atlantis at noon.’ [MA, part 2, 70, 177]
This explains, perhaps, why the Singhalese, the heirs of the Rākshasas and Giants of Lanka, and the direct descendants of Singh, or Leo, became connected with Sancha dwipa or Poseidonis (Plato’s Atlantis). Only, as shown by Mackey’s ‘Sphinxiad,’ this must have occurred about 23,000 years ago, astronomically; at which time the obliquity of the ecliptic must have been rather more than 27 degrees, and consequently Taurus must have passed over ‘Atlantis’ or ‘Sancha dwipa.’ And that it was so is clearly demonstrated. [MA, part 2, 70]
Note
According to S.A. Mackey (whom Blavatsky is quoting), 23,000 years earlier
(i.e. around 23,180 BP) the axial tilt was just over 27°, the summer solstice
point was in the Pleiades, Regulus was on the celestial equator, Taurus was
vertical to the island of Atlantis at noon, and Leo was vertical to Ceylon (Sri Lanka)
at sunset.
Astronomical calculations based on the assumption that the axial tilt is declining at the rate of 4° per 25,920 years confirm that all this is roughly true. In 23,180 BP the axial tilt was 27.02°. Alcyone had an ecliptic longitude of 98° and a right ascension of 99°; the summer solstice point, by definition, has an ecliptic longitude and right ascension of 90° (ecliptic longitude and right ascension are measured eastward from the vernal equinoctial point, along the ecliptic and celestial equator respectively). (It’s useful to bear in mind that a clenched fist held at arm’s length is roughly 10° wide.) Regulus was about 3° below the celestial equator.
At the summer solstice, stars with an ecliptic longitude or right ascension of 90° (6 hr) will be vertical at noon, and stars with an ecliptic longitude or right ascension of 180° (12 hr) will be vertical at sunset, provided the location in question has a latitude roughly equal to the stars’ declination (i.e. their angular distance north or south of the celestial equator). In 23,180 BP Aldebaran (the brightest star in Taurus, near the middle of the constellation) had a right ascension of 7 hr 16 min, and Regulus (the brightest star in Leo, in the western part of the constellation) had a right ascension of 12 hr 18 min. Mackey assumes that Atlantis (or ‘that part of Atala near Teneriffe’) was located at 24° to 28° north latitude, while Sri Lanka is located at 6° to 10°N. In 23,180 BP, Aldebaran had a north declination of 22° and, as already said, Regulus had a south declination of about 3°. Other stars in these two constellations are 10 or more degrees higher (more northward) in the sky. (See part 1, sections 1 and 2 of this article; Astronomical puzzles; Earth’s meteoric veil, appendix 1.)
SD 2:431-6
Among other arts and sciences, the ancients – ay, as a heirloom from the Atlanteans – had those of astronomy and symbolism, which included the knowledge of the Zodiac.
As already explained, the whole of antiquity believed, with good reason, that humanity and its races are all intimately connected with the planets, and these with Zodiacal signs. The whole world’s History is recorded in the latter. In the ancient temples of Egypt this was proved by the Dendera Zodiac; but except in an Arabic work, the property of a Sufi, the writer has never met with a correct copy of these marvellous records of the past, as also of the future, history of our globe. Yet the original records exist, most undeniably.
As Europeans are unacquainted with the real Zodiacs of India, nor do they understand those they happen to know (witness Bentley), the reader is advised, in order to verify the statement, to turn to the work of Denon (Travels in Egypt, Vol. II.) in which, if understood, the two famous Egyptian Zodiacs, can be found and examined. Having seen them personally, the writer has no longer need to trust to what other students – who have examined and studied both very carefully – have to say of them. As asserted by the Egyptian Priests to Herodotus, who was informed that the terrestrial Pole and the Pole of the Ecliptic had formerly coincided [MA, 2], thus was it found and corroborated by Mackey.* [*‘The Mythological Astronomy of the Ancients Demonstrated’ by a strangely intuitional symbologist and astronomer, a kind of self-made adept of Norwich, who lived in the first quarter of this century.] For he states that the Poles are represented on the Zodiacs in both positions, ‘And in that which shows the Poles (polar axes) at right angles, there are marks which prove that it was not the last time they were in that position; but the first – after the Zodiacs had been traced.’ ‘Capricorn,’ he adds, ‘is represented at the North Pole, and Cancer is divided, near its middle, at the South Pole; which is a confirmation that originally they had their winter when the Sun was in Cancer; but the chief characteristics of its being a monument commemorating the first time that the Pole had been in that position, are the Lion and the Virgin.’ [MA, 3] ...
[S]ince the Dendera Zodiac shows the passage of three sidereal years, the great Pyramid must have been built 78,000 years ago, or in any case ... this possibility deserves to be accepted at least as readily as the later date of 3,350 B.C.
Now on the Zodiac of a certain temple in far Northern India, as on the Dendera Zodiac, the same characteristics of the signs are found. Those who know well the Hindu symbols and constellations, will be able to find out by the description of the Egyptian, whether the indications of the chronological time are correct or not. On the Dendera Zodiac as preserved by the modern Egyptian Coptic and Greek adepts, and explained a little differently by Mackey, the Lion stands upon the Hydra and his tail is almost straight, pointing downwards at an angle of forty or fifty degrees, this position agreeing with the original conformation of these constellations. ‘But in many places we see the Lion (Simha),’ Mackey adds, ‘with his tail turned up over his back, and ending with a Serpent’s head; thereby showing that the Lion had been “inverted”; which, indeed, must have been the case with the whole Zodiac and every other Constellation, when the Pole had been inverted.’ [MA, 3]
Speaking of the Circular Zodiac, given also by Denon, he says:– There, ‘the Lion is standing on the Serpent, and his tail forming a curve downward, from which it is found that though six or seven hundred thousand years must have passed between the two positions, yet they had made but little difference in the constellations of Leo and the Hydra; while Virgo is represented very differently in the two. In the circular Zodiac, the Virgin is nursing her child; but it seems that they had not had that idea when the pole was first within the plane of the Ecliptic; for in this Zodiac, as given by Denon, we see three Virgins between the Lion and the Scales, the last of which holds in her hand an ear of wheat. It is much to be lamented that there is in this Zodiac a breach of the figure in the latter part of Leo and the beginning of Virgo which has taken away one Decan out of each sign.’ [MA, 3-4] ...
... The three ‘Virgins,’ or Virgo in three different positions, meant, with both, the record of the first three ‘divine or astronomical Dynasties,’ who taught the Third Root-Race; and after having abandoned the Atlanteans to their doom, returned (or redescended, rather) during the third Sub-Race of the Fifth, in order to reveal to saved humanity the mysteries of their birth-place – the sidereal Heavens. ... In Mackey’s ‘Sphinxiad’ the speculations of the bold author must have horrified the orthodox portion of the population of Norwich, as he says, fantastically enough:–
‘But, after all, the greatest length of time recorded by those monuments (the Labyrinth, the Pyramids and the Zodiacs) does not exceed five millions of years (which is not so)*; which falls short of the records given us both by the (esoteric) Chinese and Hindus; which latter nation has registered a knowledge of time for seven or eight millions of years**; which I have seen upon a talisman of porcelain. ...’ [MA, 6]
*The forefathers of the Aryan Brahmins had their Zodiacal constellations and Zodiac from those born by Kriyasakti power, the ‘Sons of Yoga’; the Egyptians from the Atlanteans of Ruta.
**The former, therefore may have registered time for seven or eight millions of years, but the Egyptians could not.
SD 2:768
[T]here must have been a good reason why an Asiatic nation should locate its great progenitors and saints in the Ursa Major, a northern constellation. It is 70,000 YEARS, HOWEVER, SINCE THE POLE OF THE EARTH POINTED TO THE FURTHER END OF URSA MINOR’S TAIL [MA, part 2, 74]; and many more thousand years since the seven Rishis could have been identified with the constellation of Ursa Major.
See part 3, section 1, note 14.
SD 2:785-6
Astraea, the goddess of justice, is the last of the deities to forsake the earth, when the gods are said to abandon it and be taken up into heaven by Jupiter again. But, no sooner does Zeus carry away from earth Ganymedes (the object of lust, personified) than the father of the gods throws down Astraea back on the earth again, on which she falls upon her head. Astraea is Virgo, the constellation of the Zodiac. Astronomically it has a very plain significance, and one which gives the Key to the occult meaning. But it is inseparable from Leo, the sign that precedes it, and from the Pleiades and their sisters, the Hyades, of which Aldebaran is the brilliant leader. All of these are connected with the periodical renovations of the earth, with regard to its continents – even Ganymedes, who in astronomy is Aquarius. It was already shown that while the South Pole is the pit (or the infernal regions figuratively and cosmologically), the North Pole is geographically the first continent; while astronomically and metaphorically the celestial pole, with its pole star in heaven, is Meru, or the seat of Brahmā, the throne of Jupiter, etc. For in the age when the gods forsook the earth and were said to ascend into heaven, the ecliptic had become parallel with the meridian, and part of the Zodiac appeared to descend from the north pole to the north horizon. Aldebaran was in conjunction then with the Sun, as it was 40,000 years ago, at the great festival in commemoration of that Magnus Annus, of which Plutarch was speaking. Since that year (40,000 years ago) there has been a retrograde motion of the equator, and about 31,000 years ago Aldebaran was in conjunction with the vernal equinoctial point. The part assigned to Taurus, even in Christian mysticism, is too well known to need repetition. The famous Orphic hymn on the great periodical cataclysm divulges the whole esotericism of the event. Pluto (in the pit) carries off Eurydice, bitten by the (polar) serpent. Then Leo, the lion, is vanquished. Now, when the Lion is in the pit, or below the south pole, then Virgo, as the next sign, follows him, and when her head, down to the waist, is below the South horizon – she is inverted. On the other hand, the Hyades are the rain or Deluge constellations; and Aldebaran (he who follows, or succeeds the daughters of Atlas, or the Pleiades) looks down from the eye of Taurus. It is from this point of the ecliptic that the calculations of the new cycle were commenced. The student has to remember also, that when Ganymedes (Aquarius) is raised to heaven (or above the horizon of the North Pole) Virgo or Astraea, who is Venus-Lucifer, descends head downwards below the horizon of the South Pole, or the pit; which pit, or the pole, is also the Great Dragon, or the Flood. Let the student exercise his intuition by placing these facts together; no more can be said. [MA, 43-8]
BCW 14:365-8
In an article entitled ‘Secret cycles’, not published in her lifetime,
Blavatsky refers to Mackey as ‘an unknown but very clever amateur astronomer’,
and adds: ‘His theory about the Hindu yugas and their length is curious – as
being so very near the correct doctrine.’ This is followed by a very
lengthy quotation, extracts from which are given below:
Note: Mackey published a booklet containing this passage in 1826/27, entitled A Reply, intended to be made to the various disputants, on an essay on chronology, which was read at The Philosophical Society of Norwich, containing astronomical proofs that the sun stood still and hasted not to go down for the space of a day, and that the shadows of the sun-dials went backwards 10 degrees.[In Hindu scientific books] we find the heavens and the earth divided into five parts of unequal dimensions, by circles parallel to the equator. ... [F]rom them arose the division of their Mahā-Yuga into its four component parts. Every astronomer knows that there is a point in the heavens called the pole, round which the whole seems to turn in twenty-four hours; and that at ninety degrees from it they imagine a circle called the equator, which divides the heavens and the earth into two equal parts, the north and the south. Between this circle and the pole there is another imaginary circle called the circle of perpetual apparition: between which and the equator there is a point in the heavens called the zenith, through which let another imaginary circle pass, parallel to the other two; and then there wants but the circle of perpetual occultation to complete the round. ... No astronomer of Europe besides myself has ever applied them to the development of the Hindu mysterious numbers. We are told in the Asiatic Researches that Yudhishthira brought Vicramāditya to reign in Cassimer, which is in the latitude of 36 degrees. And in that latitude the circle of perpetual apparition would extend up to 72 degrees altitude, and from that to the zenith there are but 18 degrees, but from the zenith to the equator in that latitude there are 36 degrees, and from the equator to the circle of perpetual occultation there are 54 degrees. Here we find the semi-circle of 180 degrees divided into four parts, in the proportion of 1, 2, 3, 4, i.e., 18, 36, 54, 72. Whether the Hindu astronomers were acquainted with the motion of the earth or not is of no consequence, since the appearances are the same; and if it will give those gentlemen of tender consciences any pleasure I am willing to admit that they imagined the heavens rolled round the earth, but they had observed the stars in the path of the sun to move forward through the equinoctial points, at the rate of fifty-four seconds of a degree in a year, which carried the whole zodiac round in 24,000 years; in which time they also observed that the angle of obliquity varied, so as to extend or contract the width of the tropics 4 degrees on each side, which rate of motion would carry the tropics from the equator to the poles in 540,000 years; in which time the Zodiac would have made twenty-two and a half revolutions ... or what amounts to the same thing, the north pole of the ecliptic would have moved from the north pole of the earth to the equator. ... Thus the poles become inverted in 1,080,000 years, which is their Mahā-Yuga, and which they had divided into four unequal parts, in the proportions of 1, 2, 3, 4, for the reasons mentioned above; which are 108,000, 216,000, 324,000, and 432,000. ...
[For the pole to return to its original position] must have taken 2,160,000 years: and this is what the Hindus call the Prajanatha Yuga. ...
Enough has been said to prove that the Hindu books of science are not disgusting absurdities, originated in ignorance, vanity, and credulity; but books containing the most profound knowledge of astronomy and geography. ...
S.A. Mackey, Mythological Astronomy of the Ancients Demonstrated,
Norwich, 1822/23 (Wizards Bookshelf, 1973)
Pages 2-6
Of the Antiquity of Egypt.
This Country, though now in the most degraded state, shews, by its monuments, that, it must have once been the Mistress of the Universe – as Rome formerly was of Europe. And yet even here, I have never been able to trace, by the monuments which have come within the compass of my knowledge, a higher antiquity than about four millions and a half of years.We are told by Herodotus, that, the CHOEN or men of learning in this country, informed him, that, the Pole of the Earth and the Pole of the Ecliptic had formerly coincided. I have seen, in Denon’s second volume of Travels in Egypt, [p. 3] two ancient Zodiacs, from a temple in Tentyra or Dendera, where the Poles have been represented in both situations: and in that which shews the Poles at right angles, there are marks which shew, that it was not the last time they were in that position: but the first. Capricorn is, therein [i.e. in the rectangular zodiac], represented at the North Pole; and Cancer is divided near its middle, at the South Pole; which is a confirmation that, originally they had their winter when the Sun was in Cancer. – But the chief characteristics of its being a monument commemorating the first time that the Pole had been in that position, are, the Lion & the Virgin.
The Lion is, therein, drawn, standing upon the Hydra; and his tail is almost straight, and pointing down in an angle of 40 or 50 degrees. Which position very well agrees with the original formation of those Constellations. But, in many places[*], we see the Lion with his tail turned up over his back, and ending with a Serpent’s head; thereby, shewing that the Lion had been inverted: which, indeed, must have been the case with the whole Zodiac, and every other Constellation, when the Pole had become inverted.
[*Note:
R.C. Leonard mentions the Arezzo Chimera of the Etruscans as an example (Quest for Atlantis, Manor, 1979, pp. 220-1). This celebrated work in bronze, discovered at Arezzo in 1534, has the body of a lion, a goat’s head springing from its back, and a serpent for a tail, though the latter is said to be a modern restoration. The goat’s head, pierced through the neck, is already dying, and the rest of the creature is writhing in agony from this and another wound it has received from the spear of Bellerophon. A lionlike creature in the circular zodiac of Dendera, which some believe represents Lupus/Centaurus rather than a second Leo, also has its tail turned up over its head, though the tail does not end with a serpent’s head (see appendix 5, figures 2 and 3).]The Chimera of Arezzo.
There is also, in Denon’s second volume, a circular Zodiac, where the Lion is standing on [p. 4] the Serpent, and his tail forming a curve downward: from which we find, that, though six or seven hundred thousand years must have past between the two positions, yet they had made but little or no difference in the Constellations of Leo and the Hydra; while Virgo is represented very differently in the two – in the circular Zodiac, the Virgin is nursing her Child: but it seems that they had not had that idea when the Pole was first within the plane of the Ecliptic; for in this Zodiac [i.e. the rectangular zodiac], as given by Denon, we see three Virgins between the Lion and the Scales; the last of which holds, in her hand, an ear of wheat. It is much to be lamented, that, there is in this Zodiac, a breach of the figures in the latter part of Leo and the beginning of Virgo, which have taken away one Decan out of each sign.
There are three Monuments in this Country, which shew that the Poles have been three times within the plane of the Ecliptic. These are the Labyranth, the column called Cleopatra’s Needle, and their Abraxes.
THE LABYRANTH
Has been described by various Authors, who agree, in stating, that, it was a Building full of [p. 5] intricate windings and turnings; and containing between three and four thousand little chambers. They likewise agree in stating that the chambers were in rows, facing inwards to winding Allies, which went round the Building, ascending and winding from the surface of the Earth; forming a spiral line from the middle upwards; and descending and winding, forming a spiral line from the middle downwards. Which is precisely the figure described by the North and South Pole of the Earth, in passing from the Ecliptic, till they coincide with the North and South Pole of the Heavens – describing at once, the precession of the Equinoxes, and the diminution of the angle of the Poles.Who can, here, mistake the design of this, hitherto, mysterious Building? Other nations have registered the rounds made by the Equinoctial points, and have given us the same number; each, in a way peculiar to itself: but none has imitated nature with so much simplicity as the people of Egypt.
But the Historians inform us that there were three Spiral Allies, and three tiers of little chambers, which shew, that the Pole had repeated its ascent and descent three times: and we find the [p. 6] Symbol of the sun (i.e. the Hawk) is placed three times upon the top of Cleopatra’s Needle. And we find the Bull there as often: as if the Bull had been as often at the Pole. And if it be true that the Gem called Abraxes, has marks about it which proves it to have been three times repeated, then, their Abraxes proves, that, the Bull had been three times at the Pole: for its name means THE BULL AT THE POLE; and is compounded of ABIR the Bull, and Axis the Pole. ...
But, after all, the greatest length of time recorded by those monuments does not exceed five millions of years: which falls short of the records given us both by the Chinese and Hindoos: which latter nation has registered a knowledge of time for seven or eight millions of years: which I have seen upon a Talisman of Porcelain, which is now in this city.
Pages 38-9
21. AXIEROS &c. – These were the distinctive appellations given by the ancients to the two poles, which were called, conjointly, the Cabirim: by which, was understood powerful gods ...
They are called the most powerful of all the gods. But let us see in what that power consists. Their name of Cabirim, is the measure of the heavens: it is compounded of Cab, a measure; and Irim or Urim the heavens; thus Cabirim is the measure of the heavens.
It is said they are the most powerful of the gods. [p. 39] Their distinctive names imply principle of generation: for, what we now understand by the word sex, was formerly understood by ax; which by being spoken with vehemence, has, in our time, settled into sex. (see Encyclo. Londinen at the word aspiration.) Now, if we give the aspirated sound to Axieros, it would become sax, or Sexieros; and the other pole would be Sexikersa. The two poles would thus become the generators of the other powers of nature – they would be the parents of the other powers; therefore, the most powerful.
But independent of these derivations, do we not know that the pole of the heavens, generates the seasons according to the angle with which he penetrates the centre of the earth, – when parallel, we have constant spring; but when he penetrates through the equator; the ravages of the elements, must be dreadful!
Pages 40-1
Herodotus, in his Thalia, number 77 records, that, when CAMBYSES entered the Temple of the Cabirim in Egypt, he derided the indecent appearance of the personified poles. Indeed I do not see how any man could refrain from laughing, beholding a man, in an erect position, accompanied by a woman whose position was inverted, and surrounded by attributes of the most [p. 41] whimsical and fantastical kinds. Seeing the woman’s head by the feet of the man, Cambyses did not know that it was intended to commemorate the passing of the original North Pole of the Earth, to the South Pole of the Heavens! But the Egyptians had various ways of representing the angle of the Poles. In ‘Perry’s View of the Levant’ there is a figure representing the South Pole of the earth in the constellation of the Harp. In which the poles appear like two straight rods, surmounted with hawks wings to distinguish the north from the south. But the symbols of the poles, which modern folly has denominated powerful Gods are, sometimes, in the form of serpents, with the heads of hawks to distinguish the north from the south end.
Page 42
Eusebius informs us also, that the Egyptians represented the universe by a sky-coloured and fiery circle, with a serpent having the head of a hawk, reaching from side to side, something like the Grecian theta; or like the diametre to the circle. Here we see the pole of the earth within the plane of the ecliptic, attended with all the fiery consequences that must arise from such a state of the heavens: when the whole Zodiac, in 25,000 years, must have ‘redden’d with the solar blaze;’ and each sign must have been vertical to the polar regions.
This great truth cannot be ascertained with too much certainty: for it will give us the master key to the ancient mysteries ...
Pages 43-8
We are told that the Gods forsook the earth – and that Justice or Astrea was the last of all the celestial train that was taken up into heaven. And when Jove took Ganimede up into heaven, then Astrea was thrown down and fell head foremost upon the earth! ...
[p. 44] The stories of the Pagans concerning the ascension of their gods into heaven, and their descent into hell, have produced, in the minds of modern Europeans the most absurd notions, – notions that never entered the minds of the first Astronomers, who divided the heavens into three grand divisions, in the most simple manner imaginable: they observed, towards the north, that a certain circuit in the heavens always appeared above the horizon; this they denominated one great empire; and as there is a point in the middle of it which is always stationary, this they made the seat of Empire, and subjected it to the government of a Monarch, who could from his throne, i.e. the Pole, behold all the nations of the earth, both by night and by day.
They could not but be sensible of that part of the vast concave that is for ever hid from our sight, surrounding the south pole; this was distinguished as another grand division of the flame besprinkled concave, and called the PIT in contra-distinction from the opposite, which was called the MOUNTAIN. Hence, among the ancients, arose the epithets of HELION and ACHERON, which meant nearly the same; as Heli-on is the Sun in his highest: which the Greeks pronounce Heli-os – i.e. Elios, the most high. Acheron, is [p. 45] generally translated Hell. It is compounded of Achari, i.e. the last state or condition; and On, the Sun, Achar-on, signify the last state, or condition of the sun: alluding to his annual disappearance in those constellations which were in the neighbourhood of the south pole. I have seen, in Denon’s 2nd vol. a zodiac with a Crab at the south pole; but the time of the greatest splendour of the Egyptians, was about 2000 years before that time; when Leo must have been there. The celebrated Orphic hymns are made to deplore the loss of Euridice in the regions below. Euridice is generally understood to be the wife of the ancient poet – ’twas the theme of which he wrote – ’Twas his Muse &c. But let us see for whom or for what this imaginary Poet of the ancients lamented, while Pluto held the object of his delight in his bottomless abyss. It was for Ari-dacah, i.e. the poor Lion – the vanquished Lion. The Greeks, who could not pronounce the Phenician term Aridaca, softened it into Euridice, and said that it was the Poet’s Wife, that had gone down into the regions of misery. The Jews, however, whose language is similar to that of the Phenicians, inform us that Benaiah, i.e. the Son of God, slew a Lion in the midst of a pit in the time of snow! Now, when the Lion was in the Pit, i.e. at the south [p. 46] pole; then, as Virgo is the next sign, her head and shoulders must have been lost below the south horizon: meanwhile Aquarius, with his pitcher of water, was at the north pole. This was Ganimede the cup-bearer of Jove, who was taken up into heaven when the celestial virgin was thrown head fore-most upon the earth!!!
Thus, we see, that, the precession of the equinoctial points, mov’d, when the pole of the earth was in the plane of the ecliptic, just as they do in our time! And that, while one sign was sinking into the bottomless pit another sign was ascending into heaven, i.e. rising up towards the pole.
As the people on the earth are insensible of the motion of the earth, they thought that the pole of heaven revolved round the pole of the earth. And if we assume a time when the poles were parallel: the pole of heaven, in eight times 25,000 years, would seem to have described a pericyclosical figure round the pole of the earth like a serpent coiled eight times; and as each volve is four degrees asunder, the figure of the serpent described by the pole of heaven round the pole of the earth in 200,000 years would sweep a circle, the diameter of which would be 64 degrees [p. 47] i.e. 32 deg. above the pole, and 32 below it: and would be found to touch the northern horizon in the latitude of 32 degrees. In that age, at noon, the ecliptic would be parallel with the meridian, and part of the Zodiac would descend from the north pole to the north horizon; crossing the eight coils of the serpent, which would seem like an imaginary ladder with eight staves reaching from the earth up to the pole, i.e. the throne of Jove! Up this ladder then, the Gods, i.e. the signs of the zodiac, ascended and descended! The Hebrew Historians relate that one of their Patriarchs saw a ladder which reached from earth to heaven, on which he saw some non-descript beings called Angels ascending and descending. It is more than 400,000 years since the Zodiac formed the sides of this ladder. Could the Pagans borrow this notion from the Jews: or did the Jews receive some feint traces of antiquity from their masters?
22. ALDEBARAN. – The names given to this brilliant star shew the uses to which it was applied by the ancients in all parts of the world. Its name of Aldebaran, signify rule or guide. It was called by the Latins Palilitium, which signifies the rule of festivals; from pha, the mouth, i.e. proclaiming, and lilia or liloth, festivals. This [p. 48] star was in conjunction with the sun 40,000 years ago, when, they held their grand autumnal festival; from which circumstance, it is very likely to have been so called from the first; before they had observed the retrograde motion of the equator. But, after a run of about eight or nine thousand years, it was found to be in conjunction with the vernal equinoctial point. This seems to have produced a new aera in astronomy; as it is a well known fact that, the Celestial Bull is highly venerated in China, in Hindoostan, and various other parts of the world, as well as in Egypt. This bright star, so venerated by the ancients, was, from its name of guide or leader, a point in the Ecliptic from which they measured the longitude of the equator, and regulated their time: and when the equator had gone through all the parts of the Zodiac, they began a new reckoning – a new series of 1, 2, 3, &c.; ’till having counted another round of 25, or, 26 thousands of years, began again with 1, 2, 3, &c. of the third round: and so on. As a proof of their reckoning from the conjunction of the equator with Aldebaran, I shall mention two facts from the histories of China and Babylon; which are well known to all the learned in Europe. ...
Note
The ascent and descent of the zodiac constellations refers to two different
things. First, the maximum height in the sky reached by the zodiac constellations
in the course of a year, as seen from any location on earth, changes as the
axial tilt slowly increases or decreases. Second, the movement of the equinoctial
point through the constellations means that the zodiac constellation that is
highest in the sky at any particular time of the year slowly changes as well.
When the earth’s axis is upright, the ecliptic and celestial equator coincide. As the tilt increases, so does the angle between the ecliptic and celestial equator. When the tilt is 90°, the north and south celestial poles (and any polestars) lie in the plane of the ecliptic, i.e. among the zodiac constellations. Since the earth’s axis continues to precess clockwise around the ecliptic pole, it will point to different zodiac constellations in turn; some constellations will be seen to very slowly ascend towards the north celestial pole, while others will slowly descend towards the horizon. At the same time, the ecliptic (and zodiac constellations) will start sinking below the celestial pole, towards the horizon, as the axial tilt starts to decrease from 90° to 0° (or rather, increase from 90° to 180°). In the northern hemisphere, the zodiac constellations will eventually sink below observers’ north horizon (first for observers at low latitudes and then for observers at progressively higher latitudes), and become visible in the south instead. Something similar takes place for observers in the southern hemisphere.
Appendix, page 23
It is not to be expected that I can be able to decypher all the historical traits which may be registered upon these ten Avatars, that may regard their national concerns; – their peace; their wars; their national refinements, &c.; that may have happened in each Avatar, or round of the Zodiac; but it will be a great point gained to science, to shew that, ‘These poor benighted Hindoos’ have registered a knowledge of Astronomy for ten times 25,000 years since the Flood, or Age of horror in the latitude of Banares.
Appendix, pages 25-6
Now, we have seen, that the tropics would recede from the pole four degrees in each revolution from the equinoctial points; from which we know, that in ten revolutions they would be removed forty degrees. But 40 and 25 are 65. Thus then at the end of ten Avatars, or rounds of the equinoctial points, the tropic would be vertical at Benares! – The tropic would be but twenty five degrees from the equator! And as we know in our time, that the tropic is but twenty-three degrees and something less than half a degree from the equator; it has still to move two degrees and nearly half before the formation of another round or Avatar, or age; which take about 16,000 years to perform. And as we know that about 9,000 years have elapsed since the tropic was vertical at Benares, so we know that the TEN AVATARS bring down the knowledge of Astronomy to that period.
Part 2 (The Key of Urania), pages 23-4
Christian Theologians think it their duty to write against the long periods of Hindu Chronology; and in them it may be pardonable: but when a man of learning crucify the names and the numbers, of the ancients; and wring and twist them into a form, which means something quite foreign to the intentions of the ancient authors; but which, so mutilated, fits in with the birth of some maggot pre-existing in his own brain with so much exactness, that he pretends to be amazed at the discovery, I cannot think him quite so pardonable.
Part 2, pages 69-70
But we will take our leave of the Daityas, or demons of the White Island, whose king was Neptune, called by the Hindus SANC’HASURA, from sanc’ha, a sea shell: and let them remain quietly in the ocean, while we consider the latitude and longitude of the lost island, and of the remaining Mount Az-burj. It was on the seventh stage of the world, i.e. in the seventh CLIMATE or MEASURE OF HEAT, which is between the latitude of 24 degs. and latitude 28 degs. north, and this White Island, which is called, also, Adbhi’-tanaya, or daughter of the ocean, is frequently described as lying in the west; and the sun is represented as setting at the foot of Mount Azburj to fight (scorch with his vertical beams) the White Devil or White Island. From these expressions, which are very poetical, we shall be able to ascertain the longitude of this White Island of the Hindu historians, which will be found to be in that place where Plato had placed the ATLANTIS.
[p. 70] In the above accounts the Hindus speak of this island as existing, and in great power; it must therefore, have been more than eleven thousand years ago: and if we assume that time when the summer tropical colure passed through the pleiades then would Cor Leonis be upon the equator; and when Leo was vertical at the island of Ceylon at sunset. Then would Taurus be vertical at the island of Atlantis at noon. And we are informed in the A.R. [Asiatic Researches] that Ceylon was so called from singha, a Lion! And in 9th vol. p. 78, that the Ox Nandi resided in the White island! These are very remarkable occurrences which must have happened about 23,000 years ago: at which time the obliquity of the ecliptic must have been rather more than 27 degrees: and consequently Taurus must have passed over ATALA or ATALANTA.
Part 2, page 74
In one place in the A.R. it is supposed that the seven stars in Ursa-major were the seven rishas [rishis]. It is a long while since they were the seven steps on Meru: and it is still longer since they extended from LANCA to DELHI.
Men should be careful how they endeavour to support false systems. It is 70,000 years since the pole of the earth pointed to the tip of Ursa-major’s tail!
Part 2, page 177
We have seen in a former part of this work that, when the ancients rectified the heavens and the earth about 23,000 years ago, the constellation of Leo was verticle at Lanca or Ceylon, and Taurus, at that part of Atala near Teneriffe, which was called the residence of the Bull ...
Additional passages on the Dendera zodiacs
Mythological Astronomy
Part 2, page 134fn
In the CIRCULAR and OBLONG ZODIACS from the Temple of Tentyra or Dendera, we see the constellation of Aquarius represented by whole-length human figures pouring down the contents of inverted BOTTLES. In the oblong Zodiac the first Decanate has a man standing on the back of a Swan, – symbol of snow; in the third the symbol’s head is decorated with flowing feathers, which seem to indicate that the downfall from its INVERTED BOTTLES is snow.
Part 2, pages 139-41
In the oblong zodiac of Tentyra, each of the twelve signs is divided into three parts of ten degrees, and each part is represented by a human figure (with attributes expressive of his functions) called a Decan; and as each sign of the zodiac has three of these, the first of each was called a powerful leader of three. To this company of thirty-six decans they attributed the management of the seasons. These were the powers whose functions were more durable than those of the twelve Zodiacal Constellations which are still found to alter their position every 2,000 years, relative to the seasons; and to move, in that time, through a space of thirty degrees from the equinoctial points. Not so the more powerful and constant gods called the Decans, or Eloim; those of that rank which are fixed at the equator are still supposed to compel the sun to shine twelve hours a day all the world over; and those at the opposite parts of the equator constantly prepel the sun the same way through their dominions; i.e. those at the spring node will not suffer the sun to pass out of their palace the same way by which he entered; but order him to move on to the sign more northward. This is known to be the constant order of the sun, moon, and planets; which must continue till the CABIRI, the MOST powerful of all the gods, shall unite; and then the functions of the Decans are at an end; and one unbounded spring shall govern all; until A POWER MORE powerful than the Cabiri, shall cause the poles again to separate; when the seasons will again return, and the Decans again take their stations: but now, observe, all topsy-turvy turned! and what before was north, the northern pole forsakes! The Lion now, which trod beneath his feet the hydra Nile, is decorated with a hydra tail, that casts his venom over the Lion’s Back!!! And now the Decan-trio of the wintry sign, when ever the Lion comes within their reach, decoy the sprawling monster backwards down; but by such slow degrees, that in twelve visits, seen from Delhi’s plain, he still is free from Swayambhuva’s den. But steady to their dreadful word of woe, when the great twelve have ten more circling revolutions run, hell’s central Pivot strikes the Lion’s heart.
Part 2, pages 156-7
I cannot conclude my remarks on the Noachidae, or people who inhabit extensive plains in the age of horror, without observing the necessity of taking into their arched flotillas some of their most useful cattle, which must otherwise have perished: this we are certain of without a revelation! and in the oblong zodiac of Tentyra, where we find cancer at the south pole; and the divisions of Gemini crowded with seven persons all busily employed in arranging matters of some serious importance, previous to their getting into winter quarters, we find, also, in the last decanate but one, to the south pole, there is actually an OX placed in a BOAT: this is not the constellation of Taurus, for that is on the other side of Gemini, where we see him with a circle on his neck which informs us that there was a full moon in the last decanate.
Note
The figure of an ox (or cow) in a boat with six stars above it, to which Mackey
refers, is similar to the figure of a cow in a boat with a star between her
horns in the circular zodiac. The figure is generally considered to represent
Sirius. (See Appendix 5, fig. 6, no. 54, and fig. 5, no. 43.)
Part 2, pages 168-9
Abram, which was the original name of Abraham is precisely the Brama of the Hindoos: it seems that this people had a way of placing the as, of foreign words last in order, as in this word Abram; by transposing the a, it becomes brama; again, when India was conquered by the King of Egypt, they called him BRAMA Gypta: here we see the a transposed; which seem to shew that they were fond of an a terminal: but whether the meaning of the name remained the same I am not certain: we know, however, Brama was their grand name for the Deity, we know, also, that they held the Bull in high veneration, but whether there was any connexion in their minds with the Bull and Brama, I am not certain; but we know that ABIR signifies the BULL; which the Greeks corrupted into Apis: both names, however, are compounds, and are applicable to the Bull, in consequence of his being the most distinguished constellation in the zodiac, and of his being used in ploughing the ground; which last employment procured him the epithet of Apis or Ab-is – AB-ISIS, contracted: Isis with the ear of corn is the symbol of harvest, and as the bull ploughed the ground, he was the figurative father of harvest i.e. Abis from AB, father; and ISIS, harvest. In the circular and oblong zodiacs from Tentyra (both of which may be seen in DENON’s Travels in Egypt) the bull is the most distinguished of all the animals, in the solar round, he was, therefore the FATHER of the FIRES, i.e. he was Ab-irim. The bright star in that constellation, is the most brilliant of all the stars or fires in the zodiac, it was the FATHER FIRE, i.e. it was AB-IR and this etymology is confirmed by the arabic name of that bright star, which is Al-de-’bir-AN, i.e. the-great-father of fires. The city of ABBIRopolis in Goshen, and ABARis in Hindoostan were so called from the abundance of cattle.
The Two Zodiacs of Tentyra, and the Zodiac of Thebes, Norwich, 1832
pages 2-3
In speaking of the origin of the Zodiac; Mr. Goodacre observed, that modern Astronomers were satisfied that the antiquity of the Zodiac was not more than 2,200, or 2,400 years at the most; and beginning at Aries, he said the ram was placed in the zodiac, in the month of April, because in that month the lambs were produced. In May, a bull was placed in the zodiac, because in that month the cows brought forth their calves; and then, proceeding to the month of June, (fearing we may suppose, to offend the ladies) he turned the two boys into two kids, saying, that in the ancient zodiacs, the Gemini were represented by two kids, because in the month of June the goats brought forth their kids. Having filled one quarter of the zodiac, he paused before he set out for the hot month of July. In the meanwhile a man in the gallery [Mackey] asked Mr. G. if he would have the goodness to state in what zodiac those kids were to be found. He, (Mr. G.) said in the zodiac of Dendera (Tantyra). The man replied, there are two, but there are no kids in either of them. Have you seen them said Mr. G. – seen them! said the man in the gallery, yes, sir, and many other men in Norwich; we are quite familiar here, with these precious gems of ancient science, and we know that there are no kids in either of them. A long painful silence ensued, and the man in the gallery exclaimed, – you see, sir, that the people of Norwich are not quite so ignorant as you may suppose them to be. Mr. G. said the interruption was ungenteel, and hoped he might be allowed to think himself quite exonerated from any further reply, and so he went on with the next three signs, which ended with Virgo, as the month of harvest in Egypt, the month of September.
In what estimation can this man be held by those who know that the harvest month in Egypt is in the month of March, i.e. in that part round about Tentyra. Now had Mr. G. allowed the ram to have been originally an autumnal sign, he would have found the virgin, with her spike of corn, (symbol of harvest) with the sun in March, the harvest month in that country. But this great truth would have embarrassed Mr. G. who had before stated that Seth, the grandson of Adam was the first astronomer. If his Seth had known the ram as an autumnal sign, he must have lived fifteen thousand years ago.
pages 9-10
We are assured by well authenticated documents, that, Cambyses, king of Persia, who lived 2,356 years ago, conquered Egypt and Ethiopia, and murdered all the men of learning that could not escape. Hence, the origin of scientific wanderers called gypsies.
As the history of science was ... written [in the Dendera zodiacs], in a character which was known to none but those venerable men who were exterminated, all its fine shades have disappeared, but the grand outline is indestructible. – Those men, however, who are desirous of not being deceived, must be careful in their choice of books; for, already there are works in print containing corrupted zodiacs of Dendera (Tantyra) in which all the marks of their antiquity are carefully omitted.
In the time of Cambyses, Aries was a vernal equinoctial constellation, and the Crab coincided with the summer tropic; but in the zodiac A [the oblong zodiac], the winter solstitial colure divides the Crab near its middle, and the Ram must of necessity be an autumnal sign, and if we allow 25,600 years in that time for one round of the equinoctial points, half that sum 12,800, which being added to the time since Cambyses, will give 16,156 years at least, since the Crab was posited, as in the long zodiac of Tantyra, which I shall demonstrate so clearly that all who know the summer noontide sun is higher than that of winter, and that our heads are above our feet, shall be satisfied that cancer in the long zodiac of Dendra, is a winter sign.
pages 15-21
The Oblong Zodiac of Tantyra explained.
Every body knows that the summer sun rises higher at noon than the winter sun does. When the sun has acquired its greatest altitude in Summer, we say it is Midsummer, and the sun turns back again; that point then is called the Summer Tropic, the upper or highest part of the zodiac, – the top part, and when the sun has descended to his lowly place in midwinter, from that point he turns back, and that point is termed the lower tropic, the bottom of the zodiac.
Upon our globes, at this time, the constellation of Gemini is the highest point of the zodiac, and Sagittarius at the bottom; but in the time of Cambyses, the crab was at the top, and capricorn at the bottom, and as the progressive motion of the zodiac makes an entire revolution in about 25,000 years, in that time all the constellations will have been at the top in summer, and all, at the bottom in winter; therefore when we see a celestial globe, we can ascertain its antiquity by the position of the zodiac.
But the zodiac of Tantyra is not placed upon a globe: how then, are we to ascertain its top from its bottom? In Dr. Jamieson’s Celestial Atlas, is given what is there called, the Zodiac of Dendera; but in that there is not the least mark of its antiquity retained: the crab is put all on one side, and the goat is transplanted to the contrary side to the correct plate of Denon.
Other authors have given the same corrupted and mutilated engravings, said to be the zodiacs of Tentyra. For what purpose is all this cutting and slaying? Does the malignant spirit of Cambyses still haunt the science of those whom he murdered? Vain attempt! since the labours of DENON have met a kindred spirit to their own. ...
Here [in the oblong zodiac] we have the 12 constellations in two strait parallel bands, placed between two female figures embracing the whole; here is a pole with a knob at one end, indicative of the top; but to prevent doubt, the knob is placed touching the mouth of the female, and no one can suppose for a moment that the mouth in the head, was intended to represent the bottom of the zodiac;– here then at the top of this zodiac we find the goat, and at the bottom, at the feet of the figure we find the crab divided near its middle. Here then, in this celebrated zodiac, we have the most satisfactory evidence, that the crab was formerly a winter constellation, and the goat, at the top, a summer constellation; and this was the first cause of the stars in that part of the zodiac being called the goat – it was at the top of the zodiac – the top of the hill; which is the delight of the goat. It was the ‘high station’ of the sun, from which he looked down with a smile upon the earth in all his glory; as a son of Crispin from his high station, might look down upon Mr. Goodacre. Every body knows that the sun in descending from the Summer to the Winter, passes over the equator in the Autumn; and here we find the Summer sun, quitting his high station in the Goat, to arrive at his cellar in the Crab, has to pass over the equator in Autumn in the constellation of the Ram. The Ram then was an autumnal sign. How could Mr. Goodacre have the impudence to stand before an audience in this city, and assert such palpable falsehoods in the science of astronomy as he did. But he did do it. He said the zodiac of Dendera did not show an antiquity of more than 2,200 or 2,400 years at the most: but here is the zodiac itself, proclaiming an antiquity of 16,000 years at least, and he said, also, that in the zodiac of Dendera, the space now filled by the twins, was occupied by two kids. But here are no kids; here we see a group of three men and women, whose attitudes seem to express, an agreement with a fourth woman on terms of accommodation on board her husband’s boat. Well may the Cambysesians of the present day send into the world spurious zodiacs of Dendera. Do they fear that the materials of Noah and his family should be recognised in this division which Mr. Goodacre said contained two kids?
Having shown that the Ram was formerly an autumnal constellation, and that about 15 degrees of cancer was touched by the wintry tropic, I shall now proceed to notice a few things expressed on this zodiac, for which, (to use the words of Denon), I think, I shall deserve well of the learned in Europe.
We see in this plate [the oblong zodiac] one large wing on the pole, which is in the plane of the zodiac. What can that allude to? According to Eratosthenes, who was in Babylon in the time of Alexander the Great, Berosus, the Babylonian Historian, informed him that 403,000 years before that time, the pole of the earth was within the plane of the ecliptic. Here we have the testimony of another great nation, that the pole of the earth was once within [the] plane of the ecliptic. Well might the detestable monster of Persia [Cambyses] desire to destroy the sacred tower of Babel, – the only monument in that country, that commemorated the spiral motion of the pole. But let us contemplate the pole in the plate before us – the pole with one wing. The pole of the earth describes a spiral figure among the stars. Why did the sages of Egypt represent the pole with only one wing? I know of no animal in nature with one wing only. But when I was a boy, at Walton, near Languard Fort, we used to have our Winters so severe that the shop tub used to be frozen up: then the men sallied out with long fowling pieces, to shoot the wild fowl that came over our heads in vast numbers:– these were wounded in every possible way, but when one has had one of its wings broken, it described in its descent, by the use of the other wing alone, a figure in the air similar to that described among the stars by the pole of the earth!!! This one-winged pole is not in the spurious zodiacs, nor are the 37 [38] little boats, which I shall now notice.
What can these 37 little Boats have done, that they are not to be tossed about upon the billows of time? – these thirty-eight little boat-like divisions of the year, contain thirty-eight inmates, the greatest half of which holds in his hand an augurial staff, as a predictor of the weather, or perhaps other events.
In the Encyclopaedia Londonensis, at the word Egypt, are given the two above zodiacs coloured; in the long one there are but thirty-one boats, and about one-third of a boat. Perhaps the number is of no importance, for I know of no astronomical division of the year into 38 or 31 parts.
In the breach of the ceiling between Leo and Virgo, there is in Denon’s zodiac, a space of two boats, but in the Ecyclopaedia Londinensis, the breach occupies but the space of one boat, – these differences ought not to exist, even if the things are of no importance.
In the ancient history of Egypt, the City of Thebes is represented as containing the whole population of the Country round about it during the Winter, and in the inundation in the Summer; to which place the mode of travelling might be by way of the Nile; this would explain the busy group in the zodiac between the full moon in Taurus and the Beetle, or Cancer, – they were about to depart for Thebes, there to remain till the end of winter, in one instance, and the retiring of the water in the other; at which time the people would issue from their retreat to their various occupations on the land. – This going into, and coming out of Thebes annually, looks very like the story of the Flood and the Ark.
If the long zodiac A, exhibits an antiquity of more than 400,000 years, the circular one displays an antiquity of at least 540,000 years beyond that: for here we find the zodiac in the plane of the equator; in which state there would be universal Spring, and the year must then, have been sidereal, as a consequence of the great difficulty of being sensible of the true tropical year. – When our calendar was altered, ten days were left out: but in this calendar, zodiac, or planisphere, we find two months left out – Leo following Taurus. We find also in the scales, the signs of Leo and Aquarius; which shews that in that remote time they noticed the precession of the equinoctial points. We find also, that Virgo is intermixed with Leo, and the first of the three virgins has her child on her lap; the idea therefore, of the sun re-appearing in, or being born of the virgin, is of a still more remote antiquity. And as the zodiac and equator coincide, the pole of the earth and the pole of the ecliptic must also coincide; and here we find the present southern celestial hemisphere coinciding with the northern hemisphere of the earth, and Boötes, to the north of the virgin, is here placed with his corn-cutting implement in his hand, on the south side of the equator.
And Sirius, Lepus, and Formalhaut are on the south side of the ecliptic, but here we find all of them on the north side of the equator. The whole of which, are convincing proofs that the pole of the earth has been in the plane of the ecliptic, and in the plane of its axis. And there are figures in the same temple which shew a repetition of each state of the pole three times.
pages 25-6
[T]he Rev. Michael Russell ... states, that the visit of Denon in the temple [of Dendera], was too short to allow him to be very correct in his delineations of the numerous figures, and that he has not given all the stars; that many of the figures are painted of the wrong colour; and that the two female figures (which surround the long zodiac) have nothing of the Egyptian features in them – they are mere childish faces, &c. Now I have shown that all this quibbling has not altered the antiquity of the whole, for though the faces of the two female figures were the faces of infants, they are placed on their heads, and their heads are upon their shoulders, which are united by a long close dress to their well-formed feet; pointing out, as clearly as the most exact likenesses can point out the top of the zodiac from the bottom, or the summer from the winter; and of course spring from autumn. In which last we find the Ram – i.e. the Ram was an autumnal sign. And as the Goat is at the top, the Goat was a summer sign. And the Crab, or Scarabeüs, at the feet, was then a winter sign.
According to Manilius, the Crab was painted on the globes of the ancients of a black colour, and without eyes (the sockets being empty). How expressive of winter!!! But Jesuitical writers take no notice of these characteristic beauties.
The Original Design of the Ancient Zodiacal and Extra-Zodiacal Constellations, Norwich, 1834
pages 8-9
Cuviere has said much about the Zodiacs of Dendera; but what is it all, but jargon. What is all his string of quidities but a collection of sophisms to draw the mind from this plain simple truth, that the Goat is a Summer sign, and the winter Solstice is in Cancer. He also quibbles about the unequal divisions of the signs. But the whole twelve make the round, through which the Equator passes in 26,000 years nearly in our time. The unequal division of the two halves, require a serious attention. Its cause escaped me at the time of writing the Treatise on the Zodiacs of Dendera and Thebes. ... It is well known in our time, that the summer half of our year is longer than the winter half by eight days. This is a consequence of the Earth being nearer the Sun in winter than in summer. ...
But the eccentricity of the Earth’s Orbit is observed to be constantly diminishing; therefore, in taking a retrospective view of Time, the eccentricity must have been greater; and consequently, the difference between the nearer half year and the remote half year must formerly have been more than eight days. And as the perihelion point moves through the Ecliptic in something more than twenty thousand years, it must be vertical to different parts of the Earth. And when over the Equator, in Autumn, the autumnal half year would be shorter than the Spring half, or in other words, from midsummer to midwinter, the Earth would require less time than from midwinter to midsummer. Now if we examine the long Zodiac of Dendera, it will be seen why all the Goat and half the Crab with the five signs between, are on one side; while on the other side there are but five signs and a half: hence there must have been, at that time, more than eight days difference between the two half years. The cause of all which is so clearly pointed out by the two Decans in the Ram seated on flames and pointing their fingers to their mouth, expressive of thirst, that no man of science can doubt that, at that time, the place of the perihelion point was in the autumnal Ram. I say, and repeat it, the autumnal Ram. For were we to consider the Sun returning from the winter to the Ram, there could not have been that heat and thirst experienced in Spring especially in the beginning of Spring, as to warrant the two expressive Decans in Aries.
Cuviere has strung together a few Sophisms about the circular Planisphere, in order to render it perplexing, by supposing the Colure may be here, or it may be there, or, or, or, &c. but he has not displayed the least appearance of knowing, that in a Planisphere where the Equator and Ecliptic coincide, there is no Solsticial point; for all the year is Spring.
pages 21-2
The ninth month, or March, was [the Egyptian] harvest month this they very properly represented by a virgin with a ripe ear of Corn in her hand, called Spica; whilst upon the, then meridian, they placed the harvest man Bootes, with a Sickle in his hand, which touches the tail of the Bear, near a small Star called mizar which Dr. Jamieson, in his celestial Atlas, says, means the reaping hook.
This virgin is thrice repeated in the long Zodiac of Dendera, one of which holds up a wheat-ear between Leo and the Balance or Scales, in the circular Planisphere there are three virgins, which represent the three Decans, into which each sign of the Zodiac was divided. But, here, the first virgin is represented with a Child on her knee; which proves that the story of the virgin and her child, was known to the Egyptians more than a Million of years back.